Softpanorama Bulletin
Vol 24, No.10 (October, 2012)
Prev | Contents |
Next
OFM standard 1999 (basic OFM requirements) Version 3.11
Dr. Nikolai Bezroukov
Version 3.11 (revised November 2012)
Change Records
[Nov 08, 2012] New results for OFM1999 compatibility test produced.
[Nov 07, 2012] Compete revision of the standard version 3.0 produced
[Oct 18, 2012] MC 4.8.1 has problem with new implementation of Ctrl-O when on return active panel is not change even
is current directory was changed in shell.
I modified Ctrl-O description to account for this possible implementation bug.
Reverse engineering and generalizing basic functionality of OFM managers is a difficult, non-rewarding, but necessary
work. I did it because I am afraid about possible disappearance of a set of valuable ideas invented by various talented
implementers. Many of them like the Norton Commander creator John Socha and FAR creator Eugene Roshal participated in the
OFM design only for a short time (1994-1989 for John Socha, 1997-2001 for Eugene Roshal) and then completely abandoned the
field. Actually, I have a feeling that John Socha was very surprised when he read one of the versions of my
The Orthodox File Manager(OFM) Paradigm eBook :-).
Some of historically important OFM managers are now belong to abandonware (all Norton line of products, Volkov Commander,
DN to name just a few). Some are now long gone and difficult to find. And not all of them were open source. I am afraid
that without reflection in the literature in a way reusable by subsequent generation of programmers those ideas and unique
feature invented by previous generation of OFM developers will be gone and need to be reinvented again, may be in crippled
form.
I have a huge advantage to observe the field almost from the very beginning and working with several different OFM during
my more then 20 years experience with this type of file managers. At the same them the amount of time and effort I was able
to spend on this work is limited (actually the recent revision happened only due to a week long isolation produced by tropical
storm Sandy as NJ was hit really hard;-) So the result in some parts are raw. But I think that they can provide a solid
foundation to additional work and hope my efforts to create those standards will be useful for new OFM implementers including
those who are attracted to existing open source projects like FAR and Midnight Commander. Useful because to understand the
key ideas is much easier it you put all your knowledge into some framework. This standard and two subsequent standards (OFM2004
and OF2012) are imperfect, but useable framework of analyzing functionality and enhancing exiting OFM projects as well as
can save time for those who try to implement a new OFM, especially in scripting languages such as Python, Perl or Ruby.
I try to update the Orthodox File Managers Standards once in five year with the last update made in Oct-Nov.
2012. to reflect progress in OFM implementations and changes in the field. This one (OFM1999)
was the first and is now in its third revision (version 3.0). It was followed by the OFM2004
(advanced OFM implementations) and OFM2012 (Cutting Edge Features of Orthodox File
Managers). Actually the last revision of OFM1999 was done after seven years
after the second, not five due to various circumstances and the workload of the author.
Important notes:
- The Orthodox File Managers Standard does not require key assignments to be exactly the same as in Norton Commander
as long as there is a possibility to change them. All specified key binding are recommended. If semantically
the feature implemented in accordance with OFM doctrine, but there is no key remapping feature and the OFM use different
hot-key, then the compliance score for the feature is multiplied by 0.66. All Alt keys can be replaced with
Ctrl-Alt keys in Windows GUI implementations. Switching Alt to Shift for functional keys
is permitted for UNIX implementations that does not support keymapping.
- The structure of main menu is not defined in the standard, but the standard presuppose there is one.
- The capability to connect with a different computer via serial line is not included in the standard.
For inclusion into this section of the standard the feature needs to be present either in MC (as a leading Unix-based
implementation), FAR or NC 5.0 or be consistently implemented in at least two other major OFM implementations (for example
XTree virtual file system is consistently implemented in Total Commander and Northern Captain with the hotkey binding Ctrl-B)
and have stable semantics. Hotkey assignments listed below can be different from recommended, if key remapping capability
is implemented in a particular OFM, otherwise 0.66 coefficient is used if semantically operation in implemented correctly.
If the weight is not stated it should be assumed to be 3)
- Interface look & feel
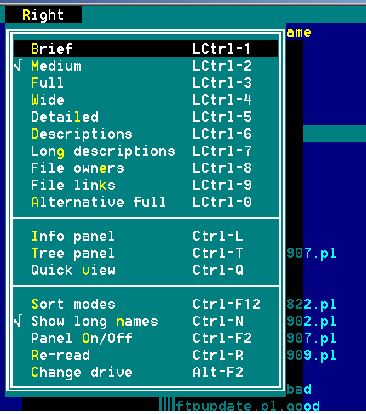
- Symmetrical panels (but controlled separately) with user definable fields in each (left and right separately)
and ability to switch to one of several predefined templates. In the picture ten templates are defined: Brief, Medium,
Full, Wide, Detailed and so on...
- Information line (infoline) should be present at the bottom of each panel, by default displaying
the current file (or overflow of the current file name, in the name column is too narrow for full name and if space
allows additional attributes not displayed in the panel view (such as ownership and permissions).
- Top and bottom menus. Top menu can be by default hidden (activated with F9 or click my mouse on the top
border) and provide with access to configuration and commands without shortcuts
- Bottom menu should be "mouse clickable" and should change the displayed key shortcuts, if you press
and hold Ctrl, Alt, Shift for "F-operations" such as F1-F9. If due to keyboard driver limitations there is
no possibility to provide change by "Press and hold" rolodex style rotate buttons should be provided.
- Ability to position panels both horizontally and vertically should be present. Unequal split between left and
right or upper and lower panels should be possible.
- Command window should be present by default in minimized form, as a single line with shell prompt. Should allow
entering multiple command in shell.
- Ability to hide left or right or both panels exposing terminal shell screen should be present
- Ability to shrink both panels 50% exposing shell terminal screen should be present
- Separate menu of settings for left and right panel
- Navigational and basic hot keys compatibility:
- Enter compatibility. If command line is not empty, then pressing Enter should execute
the current file if it has executable attribute. If not extension menu should be used for determining operation
to be performed (typically view). If command line contain one of more commands, pressing Enter should result
in their execution. They should be processed by first performing macrosubstitution of OFM variables and then executed
one by one. Results of execution should be available via scrollable command window visible via Ctrl-O
-
The Tab key should change active panel to passive and passive to active;
-
Ctrl-\ key should go to the root of logical drive (Windows), or show the list of directory favorites
(Unix)
-
Ctrl-PgDn and Ctrl-PgUp move to the upper (current subdirectory) and lower level (parent
i.e. CD ..) directories; in Unix Ctrl-ArrowLeft and Ctrl-ArrowRight can be used instead.
The importance of this feature is that it permit exit from several level of directories without changing the command
line that might contain partially typed command. This way you can assemble command line while traversing directory
for its components, for example file names. If mouse clicks on directory can be used instead for the same purpose
this feature can be judged as compatible.
- Ctrl-R / Ctrl-U compatibility. Ctrl-R -- should reread
the directory; that should work for virtual filesystems for example FTP VFS as well. Ctrl-U -- should
swap panels;
- Quick search via Alt-letter should activate instant search on the
panel: you start typing letters with alt-letter prefix and instant search using already typed prefix is performed.
- Alt-letter (or Ctrl-Alt-letter for GUI-based versions) quick search option should be
available for both regular and tree views of the panel. It should work as instant search for the typed prefix.
- Ctrl-Enter during quick search should move to the next item with given prefix
-
Alt-F1 and Alt-F2 (Ctrl_Alt-F1/F2 In Windows
should produce the list of logical drives and allow selection of any of them. In Unix should produce the list of
mount points (df -k) and allow to selection any of them.
-
Ctrl-L should switch to the information panel. Information panel should provide at least statistics
about the current directory and current drive. If directory description file (by default file dirinfo in
Windows implementations) is available it should be displayed as well (Default for dirinfo descriptions
in UNIX-based implementations should be README file). If multiple files match user-defined regular expression
specified in dirinfo, the first should be displayed. The file that serve as dirinfo file should be
user-definable with the possibility to define it with regular expression (this way multiple files can be defined,
if desirable).
-
Ctrl-Q should switch to quick view in which movement of cursor on the active panel changes the
view of the file in the passive panel.
- Shell window compatibility
- OFM should behave like tile windows manager and be able to expand command line (which is a minimized
to a single line third, borderless shell terminal window) -- to full screen, to half screen vertically, to half
screen horizontally and to quarter of the screen (half with one panel hidden):
- Command line should allow to execute multiple command from it with macrosubstitution of macrovariables
and shortcuts to the current file to the command line (Ctrl-Enter) as well as path to left and right
panels (Ctrl-[/Ctrl-]).
- Ctrl-O should maximize expand shell terminal windows to maximum size (hide both panels by default):
- In the resulting screen standard shell terminal functionality should be present as if this is a telnet session
to localhost. For example, if the shell for a particular OS provides browsing of shell history with arrow keys
this should work.
- If current directory was changed during the work in command window, the active directory in the panel should
reflect the new directory on return to panel view by pressing Ctrl-O again.
- Terminal session look& feel compatibility. Expanded window should behave like terminal session (like in
GNU screen). For bash at least the following features should be present:
- Ability to change command prompt (Unix)
- "Arrow" access to history (Unix)
- Ctrl-R search in command history (Unix)
- Ability to scroll windows back
- Change of directory in shell terminal windows leads to change of active panel directory on return to panel view.
If commands in command window changed the content of the current directory then the active panel should instantly
reflect those changes.
- Ctrl-F1/Ctrl-F2 should provide a view of the shell screen with overlaid one panel (hide one panel exposing
underling shell terminal window and results of execution of previous command, if any).
- Ability to shrink panels 50% or gradual shirking/expansion of panels (vertical shrinking compatibility
- With one panel hidden (left or right) in both half window mode and full terminal windows mode.
- Ability to expand active panel to full screen
- Compatibility of F1..F12 and other F-keys operations
-
F1 -- should not only invoke hypertext help, it should invoke help on any item of the toolbar and any
item of tool bar menus. The help should be context sensitive. HTML based format is preferable. Context help should
be implemented: if some dialog is opened the help should be about this particular dialog, not the general help tree.
-
F2 -- availability of user menu or equivalent (start menu). Should provide the possibility to
run user shell scripts with substitution of macro variables from the panels. Each item of the menu should be activated
by its own letter (hotkey). Format of the macro variables is not defined in this standard but following Midnight
Commander conventions is recommended.
- Invocation of viewer and editor.
-
F3 -- should invoke built-in viewer
- F4 -- should invoke built-in editor (optional)
-
Alt-F3 and Alt-F4 should select alternative viewer and editor. There should be a
configurable option is Command menu to specify this external viewer and editor
-
Optional: Additional option in Options menu to specify invocation of built-in viewer and editor
in the panel mode instead of full screen mode. At this mode all command line insertion capabilities should be
redirected to editor (Ctrl-[, Ctrl-], Ctrl-F, etc). switch primary and alternative
viewer, so that alternative viewer/editor can be selected via F3/F4 and primary (built-in) via
Alt-F3 and Alt-F4.
- Copy Operation
-
F5 -- should copy/move subtrees if applied to directories; Should work with selected files and permit
specifying "quick target" via F10.
- Shift-F5 should either copy file within the same directory and should gives possibility to specify
the path and name.
- Alt-F5 should create a symbolic link from the file in the current directory to the directory
in passive panel.
- Copy "overwrite" dialog windows should contain information about the size and date of creation of
files. If target is newer then source the info should be in red
- Move operation
- F6 should be able to move subtrees. Movement of directories within the same logical drive does
not result in copy operation;
- Shift-F6 should permit renaming of the file or directory with the capability of editing the old
name (not reentering it).
- Alt-F6 should create hardlink
- Copy "overwrite" dialog windows should contain information about the size and date of creation of files.
If target is newer then source the info should be in red
- F7 should create directories. Shift-F7 or similar combination should create soft link to the
current directory on active panel in the directory in passive panel
- F8 should delete files or directory subtree if applied to the directory with non-empty subdirectories.
In case the group is selected the operation is performed on each member of the group. F8 operation should
perform deletion of subtrees is it is applied to the directory with non-empty subdirectories.
- F9 and F10 -- Main menu activation and exit (For GUI versions F10 can activate menu too, instead
of exit -- this is Windows standard)
- (optional) F11/F12 compatibility. F11 -- chmod/chown, F12 -- macrorecoder
- Tree View Panel compatibility: This is a mode similar to Microsoft
File Explorer mode with some notable differences.
- Ability to copy files to the tree target (if you change passive panel to active with Tab key
or mouse and try to copy file the target will be the directory on the tree that was current).
- Movement of the cursor on the panel with tree representation should not lead to change of the directory on the
passive panel (Microsoft File Explorer mode). + and - or ArrowLeft/ArrowRight should expand collapse directories.
Enter or double mouse click should change directory of the passive panel to the current on tree
panel.
- Quick search in tree mode (Alt-letter, Ctrl-S)
with jump to directories with the same prefix down the tree. In quick search mode Ctrl-Enter should
jump to the next directory with the same prefix (If no prefix is specified it find the next directory with the same
name, if any). Note: search should be activated; in normal mode it should paste the current directory into the command
line.
- F5/F6 compatibility from tree view to passive panel.
- Same level of nesting of directories navigation. Gray+ (or spacebar), Gray- (or backspace)
should move up and down the tree to the next branch on the same level.
Alternative keys
- PgUp/PgDown can also be used for same level navigation on tree , especially in GUI based
OFM as they are pretty much useless for anything else.
- ArrowLeft, ArrowRight also can be used, especially in Unix OFMs.
- Quick view tree navigation: Invocation of Ctrl-Q on tree panel should lead to quick mode of
navigating the tree -- changing tree in one panel should make the current (highlighted) directory current on the
second (passive) panel. There should be two navigation option:
- Tree browsing. In this mode changing the directory on the active panel should lead to display of the content
of this directory on the passive panel.
- Dirinfo mode. If dirinfo file is present in the directory it is displayed. If not some statistics about
directory is displayed.
- Enter should change passive panel directory to current on tree view. Ctrl-Enter should
copy file to the command line
- F4 in treeview mode should invoke attribute changing dialog box that should allow to edit directory
attributes
- Navigation keys such as Home/End and PgUp/PgDown should work.
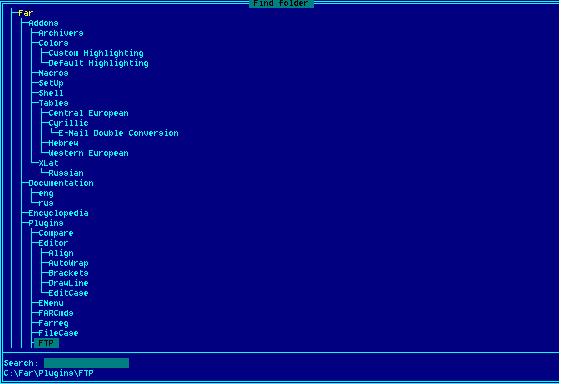
- Directory Search Panel compatibility (aka NCD panel, aka FindFolder):
The directory search panel (find folder). Activated by Alt-F10. Also should be present
as an option in the top menu as Command/Find folder in Far, Command/Directory tree in mc, ). This panel should instantly
provide a quick search window. It should be also accessible from copy/move dialogs (via F10) as it is often used
not only for the "directory completion" and traversing of the tree, but also for the quick selection of the target directory
for copy/move operations. Here for example is how FAR NCD tree looks like:
- Initial Focus of the tree. Alt-F10 or other hot key used for NCD tree should produce tree view
of the current panel starting with the current directory (not root!) and provide the ability to select new current
directory on this representation with Enter.
- Refocusing the tree( F5). You can put any directory "in focus" (position it in
the middle of the panel) by pressing F5 and simultaneously maximize panel to full screen. Pressing
F5 again will restore the window to the previous size.
- Rescanning behavior (using F2). Pressing F2 rescan the disk. Pressing Alt-F10 should not
produce rescanning of the disk without reason, but rescanning should be available as an option (usually via
Ctrl-R or F2)
- Quick search input line should be enabled automatically at the bottom of this panel - any input other
than control symbols is considered as a search prefix
- Ctrl-Enter should jump down the tree to the next directory with the same prefix.
- Copy(F5), move(F6) and FindFile (Alt-F7) operation should provide the possibility
to select the target from the quick tree search panel (preferably via F10).
- File/Directories selection/deselection compatibility:
- Ins should select a single file (cursor may move one line down if such option is set); If Ins
is pressed on already selected file it should be deselected (toggle).
- Gray+ and Gray- should select and deselect file using a regular expressions (as a minimum,
shell basic regular expressions). For example, with basic regular expressions the expression *a*.* should
select files like my_bak.tmp and my_bat.txt, not all files) (MC, FAR, Total Commander, NCW).
- Gray+/Gray- operations should be persistent (second selection operation adds to existing
selection);
- Gray * inverts the current selection
- Named (savable/restorable) selections -- projects (Total Commander)
- Select by file type, date range or custom script (FindFile-style selection) (Total Commander)
- Selections history should be available (Ctrl-Up) and browsable with the same keys as file command history
and mouse-clickable [^] icon.
- Ability to separate individual regex with ";" or "|"
- Option for extended or Perl-style regular expressions support.
- Optional:
- Shift-Grey+ / ShiftGrey- select all and deselect everything regardless of the current
selection (This can be done using asterisk in regular selection)
- Restore Selection operation (no standard key exist, Ctrl-M (FAR) can be used ). It should
restore highlighting of files selected for last copying operation.
- Quick view compatibility:
- Panelized Build-in viewer should be invoked for all files. Depending of type files are displayed
either in text view or hex view. Moves of the cursor up and down in the current panel in quick view mode should
change the content of the current file in the passive panel with the viewer ( Infopanel)
- For archive basic stats and content of the dirinfo file should be shown (list of information files should
be customizable with a regular expressions (or a set of regular expressions), but default should include
File_id.diz, README, read.me, readme.1st). In case no description is available
the top part of the toc of the archive should be shown.
- For directories basic stats and dirinfo file should be displayed. Behavior should mirror the behavior for
archives. Stats should include number of subfolders, files and total subtree size in bytes. Here is an
example from FAR:
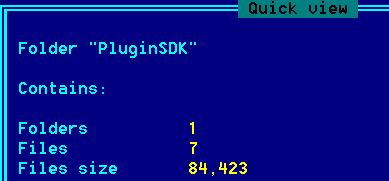
- For executables the header should be shown. In windows typical ownership info should be displayed, if it is
present. There should be capability to invoke a script on exec files.
- If there are selected files exit from the internal viewer in info panel via F3 should display the next highlighted
file, not the next file
- In tree view Windows File Explorer mode should be implemented: ability to view files in a new current directories
on each movement of the cursor tot he directory as in Windows File Explorer
- Macro recorder compatibility
- Keyboard macros should be available in panel view and editor.
- Ability to edit macros
- Availability of internal macrolanguage with conditional constructs and loops
- Macro can overwrite standard key assignments
- FindFile compatibility (Alt-F7)
- Reversible implementation of at least View( F3 and edit (F4) -- after exiting user return
to the search panel without researching; irreversible implementation of Jump (Enter).
Please note that search can be used as a poor man command completion in the current directory: it's very convenient
for files with long names and for search operation and essentially bridges search operation and wide (double-width)
panel representation.
- Unix find search expressions or equivalent should be supported. Here is example of FindFile dialog from FAR:
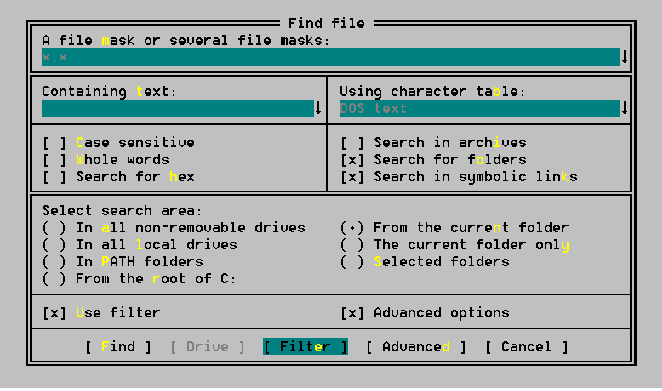
- The ability to search by content (regular expression like in Grep)
- Search history
- Panelize option or availability of all other file operations directly from the search panel (optional
if Script-based VFS is implemented as in MC); Refresh (Ctrl-R) should work for panelized view. All file
operations should work with the panel.
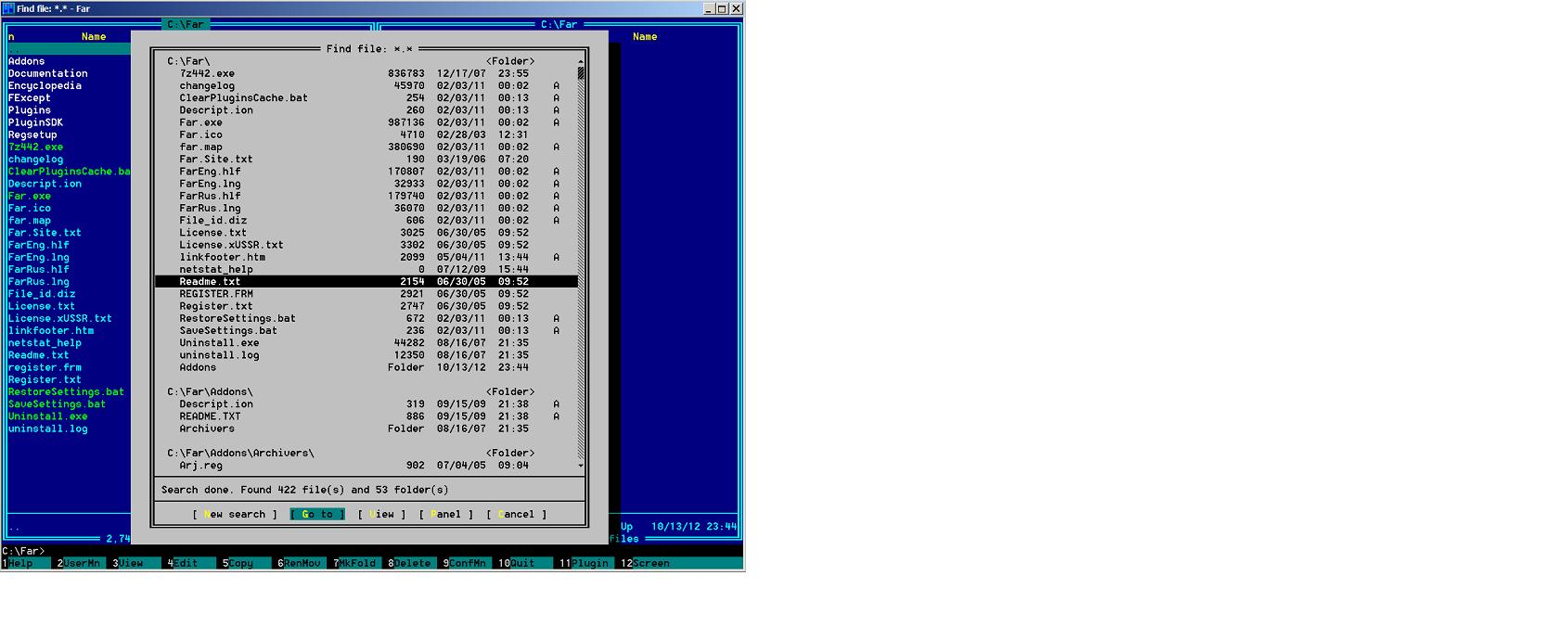
- Quick selection of the start directory using tree search panel (F10)
- Command line execution compatibility:
- The ability to view the results of shell command execution by hiding both panels using special hotkey
(usually Ctrl-O) It should also work the same way from built-in viewer and editor.
Note: NC it was also possible to shrink panels to 50% providing visibility of shell execution as well
as subset of files in panels. This feature was never implemented in most OFMs and as of October 2012 removed from
the minimal standard.
- Cursor movement keys should work like in OS shell when panels are hidden
- Change of the current directory via command or script execution changes the directory on the active panel;
- The "special paste" operation compatibility. The following operation should be supported for command
line (minimized shell window) mode:
- Inserting current path from left and right panels (Ctrl-[ and Ctrl-])
- Inserting the current file with Ctrl-Enter (if one or several files are selected
they should be inserted into the command line instead of the current). Same with full path Ctrl-Shift-Enter
- Inserting the list of selected file on the current panel
- Optional
- Inserting the current file from the passive panel (Ctrl-F)
- Inserting the current file with abs path from the passive panel
- Sorting directories compatibility:
- The ability to view files (and optionally directories, but directories should generally precede files) sorted
by name, time, size, and unsorted order (minimum is "NETSU" (sorting by Name, Extension, modification
Time, Size, and Unsorted). The ability to sort by creation time, access time and descriptions
is optional. For Unix, the ability to sort by permissions, owner and group is recommended ("NETSUPOG").
- Directories first option should be provided.
- Mouse click on any header (name, size, time, etc) in the panel view should change the sorting order for this
attribute. Second mouse click on the same button reverses the sorting order (Windows Commander 3.03; NCW 1.0);
- Sorting Groups (aka sorting mapping function) should be available, for example, directories, or
(htm|html|shtml) as one group.
- Ctrl-I should proved the ability to define named file panel filters.
Here named means that those filters that you have given a name will be saved on exit and restored
on reentry (FAR) so that they can be reused in other sessions:
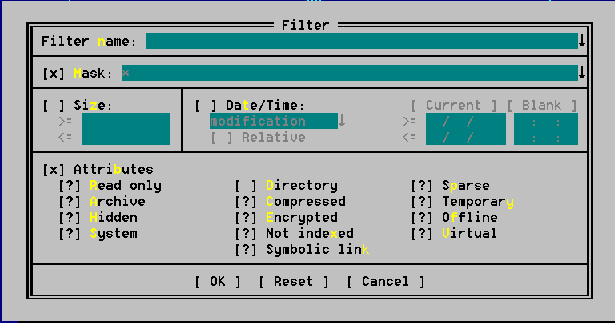
- Ability to name filters and save restore named filter should be provided (FAR)
- User menu script invocation compatibility (GUI implementations can provide alternative
methods to run custom scripts with parameters taken from the panel):
- The ability to specify the hotkey and the label for each script
- Hierarchy of user menu files (local/user/global)
- Multiple commands can be written without need to create a separate batch file
- Include files should be permitted in the user menu (hierarchical menu)
- The ability to use macros for elements from both passive and active panels in user menu commands (the current
file, the selected files, the current path are minimum, MC schemes are recommended, while NC-style is deprecated:
- The MC-style naming system for macro substitution symbols for active panel (see below the set for
passive panel)
- "%f" The current file name.
- "%F" The current file in the unselected panel.
- "%d" The current directory name.
- "%D" The directory name of the unselected panel.
- "%t" The currently tagged files.
- "%T" The tagged files in the unselected panel.
- "%u" and "%U" Similar to the %t and %T macros, but after the operation
all selected files are untagged. That means that this macro can be used only once per menu entry (or extension
entry), because on the second and subsequent invocations there will be no tagged files.
- "%s" and "%S" The tagged files if there are any. Otherwise the current file.
- "%cd" This is a special macro that is used to change the current directory to the directory
specified in front of it. This is used primarily as an interface to the VFS.
- "%view" the invocation of the internal viewer. An argument to force the viewer in a particular
mode can be passed: ASCII to force the viewer into ASCII mode; hex to force the viewer
into hex mode;
- "%%" The % character
- "%{some text}" Popup an input box and prompts for the substitution. The user should
be able to cancel input ( ESC or F10 recommended).
- Note: Instead of Case change method for macrovariables in active and passive panels (as in
%f and %F) there can be a special prefix that turns macro symbols for active panel to
macro symbols to passive panel, if applicable, for example %f is the current file name on active
panel but %-f is the current name on the passive panel.
- NC-style naming system for macro substitution symbols in OFMs (not recommended for Unix implementations,
they should use mc-style symbols, see above). At least the following macro symbols should be defined:
! The current file name without extension
!.! The current file name with extension
^! The current filename of the passive panel without extension
^!.! The current filename of the passive panel
!& List of names of selected files
!: The current drive
!\ or !/ The current path
Some prefix or suffix (for example ^) can be used to define the same macros for the passive panel to refer to
the passive panel.
NC style is deprecated and should be avoided in new implementations of OFMs
- Additional file commands compatibility:
- File attribute command (no hot key specified, should be available via menu) should permit changing of attributes
and file stamps of a single file or group of files, or subtree (if applied to the directory) as well as ownership
(in Unix);
- File timestamps editing
- File ownership
- Rename tool
- Diff tool
- File case conversion command should permit changing of the case of the file or group of files (not applicable
to DOS implementations)
- Association (extension menu) management compatibility:
- Multiple associations. The ability to specify one or several associations for the same extension using regular
expressions
- Internal editable file that take precedence over system associations
- Hierarchy of association files (global/user)
- Ability to specify actions for View, Edit and Enter operations in the same file
- Usage of regular expression in determining the association
- Ability to use file type instead of file name (as returned by Unix file command)
- The ability to use the same macrovariables in associations in the file association table as in the user menu.
- Compare directories:
- Simple attributes comparison
- Comparison rules/filters should be provided (only size, only date, etc) generally equivalent in capabilities
to search. Can be provided as a different command (synchronize command like in Total Commander)
- Strong comparison (comparison by equivalence of file content, possibly using MD5) should be provided.
- Option to ignore date of creation and other data stamps (important for FTP VFS)
- Synchronize option or command
- Built-in viewer:
Note: Should be able to work in full screen mode and in
panel mode (at least in quick view).
Optional: User should be able to invoke the viewer in the panel mode not only in quick view, but also via some hotkey
(for example Alt-F3). This is very useful if 132 screen mode is used.
- End should go to the end of the file; Home to the beginning of the file;
- Wrap/unwrap feature (F2);The ability to view file in hex should be provided (via F4)
- Ctrl-O shows command line screen
- The ability to search for regular expression (F7); to repeat search (Shift-F7).
- "/" and "?" keys should serve as additional hotkeys for regular expressions
search forwards/backwards as in many Unix tools.
- The ability to search in reverse direction (Alt-F7 or Ctrl-Alt-F7);
- Pressing F3 should exit the viewer -- very convenient key assignment for quick exit from the viewer (MC,FAR);
- + should go to the next file, - to prev
- Bottom menu changes when Ctrl and/or Alt is pressed.
- Bookmarks for file positions should be available
- Ability to go to specific line number and specify offset in percents
- Optional: mouse click on the current line number should open panel to specify line number to go.
- Built-in Editor
- Look and feel
- The bottom menu changes when Ctrl or Alt keys are pressed;
- The ability to view hex representation of the current symbol in the upper menu;
- Top menu provided with F9 and replaces information line
- Syntax highlighting
- DOS/Unix compatibility
- Autodetection of Unix/Dos style text files and preservation of the style in save.
- Ability to change style on save.
- Windows style way of selecting blocks of text. Shift-Arrow should select line block;
- Special hot key to go to a line number (Ctrl-G). Optional: mouse click on the current line number
should open panel to specify the line number to go.
- Hotkey for finding matching bracket should be provided.
- Open/Close/Save compatibility
- The ability to create new file (Shift-F4) instead of editing current;
- F2 - Save changes without exiting; Shift-F2 save with new name (SaveAs);
- Esc,F10 - Exit (should produce save prompt if changes were made); Shift-F10
- save and exit.
- Search compatibility. The ability to search for text string and regular expression in search option (F7)
and repeat search option (Shift-F7); Optional: Search for same text in reverse direction;
- Basic keys compatibility
- Backspace - Delete character left of the cursor; Ctrl-Backspace - delete word left of
the cursor
- Del - delete character under the cursor; Ctrl-Del - delete word right of the
cursor;
- Home -- Go to start of line; End - Go to end of line;
- PgUp/PgDn - Move up/down one page;
- Ctrl-Home - Go to top of file; Ctrl-End - Go to bottom of file; Ctrl-PgUp/PgDn
might be synonyms or to top/end or go to top line/bottom line of the screen;
- Ctrl-Q -- Quote character (insertion of special characters)
- Ctrl-Y -- delete current line; Ctrl-T -- delete current word;
- Ins - Toggle Insert/Overstrike mode; Optional: hot key for Auto-indent mode;
- Ctrl-O shows command line window with the ability to execute commands.
- User menu should be provided with at least one additional macrovariable %b to allow to pipe block to the
script and insert the result of the script to the position after the cursor
- User menu. User menu should be provides with at lease one additional macrovariable (%b) allowing to insert
the test after the cursor or block and pipe the block into script.
Optional: User should be able to invoke the editor in the panel mode via some hotkey (for example Alt-F4).
This is very useful if 132 symbol terminal width is used. In panel mode all command line insertion hotkeys should
be redirected to the current position of the cursor in editor (Ctrl-[, Ctrl-], etc)
- Archive virtual file system (optional if plug-ins are supported
and corresponding plug-in provided)
- Viewing Archive VFS like regular directory. Operations view(F3), Edit(F4), copy(F5), move/rename (F6), delete(F8)
should be supported like with directories. Files can be selected, deselected as in regular folder;
- Compress/extract directories and file into/from archive. Extract command should permit creation of a folder
with the name of archive without extension for extraction ( FAR, DN).
- Navigation compatibility:
- pressing of the Enter key on the archive file should produce the listing of archive content in the panel;
- Any operation for leaving the folder should work as closing the archive view.
- Quick search (alt-<letter>) should work on archive VFS panel.
- Ability to view self-extracting archives via Ctrl-PgDn (like diving in the directory)
- Support of at least ZIP, GZIP, TAR, ISO and RAR formats.
- History and favorites compatibility.
- Command history (in panel view) should be available both via hotkey (Alt-F8)
- C-shell-style browsing mode should be available. In C-shell style browsing mode the retrieval of a command
from the history into the command line should be possible with the hotkeys, for example (Alt-E, Alt-X
like in NC5).
- The possibility of exporting command history to a flat file and retrieving command history form
the file.
- Browsable history of commands in command like in all dialogs via on [^] or Ctrl-Up
- History invocation on mouse click on [^] or Ctrl-Up
- In additions in all dialogs (For example Mark/Unmark dialogs, visited directories, viewed edited files,
etc) it should be scrollable with mouse wheel (FAR)
- Visited directories history (folder history Alt-F11 in FAR)
- Viewed and edited files history
- Directory favorites list should be available (Ctrl-\ in Unix)
- Ability to panelize history of visited/edited files (hotlist)
- Command completion: Alt-Tab or Ctrl-End at the end of the command line complete the
command starting with these symbols from the command history. In case several variant of completion are possible
they should either displayed or it should be possible to press Ctrl-End several times to find the next
command in the history that has the same prefix
- Infopanel and infoline compatibility
-
Ctrl-L should switch to the information panel. Information panel should provide at
least information about one special file defined in Options/Infopanel Settings submenu of the top menu. The default
is dirinfo in Windows implementations and README for Unix implementation, or both.
If one of defined dirinfo files is available in the directory it should be displayed in the opposite panel. There
should be the possibility to define it with regular expression (this was multiple files can be defined, if desirable).
Several file can be defined, separated with semicolons. If multiple files are present only the first is displayed.
Information panel consists of two parts upper (that is optional) and lower.
- Upper part should provide one or two lines basic statistics (total bytes in the directory, total number of files
and free bytes on the harddrive) about the current directory and current drive (see FAR as reference implementation).
- Lower half should display so called "directory description" (dirinfo) file. the latter a special file
user-definable with a regular expression. If such file is present it should be displayed in the bottom half. If
multiple files match regular expression the first match should be displayed with the capability to move to the next
match via F10. For example this was the capability
to view README file can be provided. (new in OFM2004 revision
1.3, Oct 2012).
- If infopanel is made active with Tab, all F-keys should be applicable and process the dirinfo file as a source.
F3 in this panel should switch to view of dirinfo file and F4 to its editing. On the picture below
File_id.diz serves as dirinfo file (in FAR the set of dirinfo files is fixed).
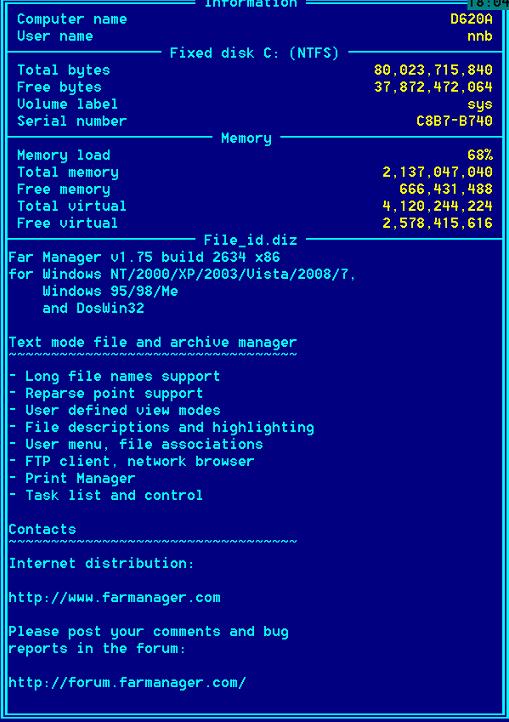
- If there is no file corresponding to regular expressions in infopanel definition additional information about
the system should be displayed. Here is an example from FAR
- For directories you should be able to view dirinfo file in full screen by pressing F3 key
- Infoline at the bottom of the panel should display file name (or "overflow" for long names) and additional (custom)
attributes.
- Extension menu definable infoline attributes similar to custom template of columns for panel
(the data are current as of November 7, 2012)
Summary
|
OFM1999 score (average of all 21 tests) |
|
NC |
VC |
DN |
FAR |
Total
CMD |
NCW |
MC |
FC |
|
Scores |
|
68 |
71 |
73 |
89 |
70 |
68 |
66 |
75 |
Detailed Results
[an error occurred while processing this directive]
Society
Groupthink :
Two Party System
as Polyarchy :
Corruption of Regulators :
Bureaucracies :
Understanding Micromanagers
and Control Freaks : Toxic Managers :
Harvard Mafia :
Diplomatic Communication
: Surviving a Bad Performance
Review : Insufficient Retirement Funds as
Immanent Problem of Neoliberal Regime : PseudoScience :
Who Rules America :
Neoliberalism
: The Iron
Law of Oligarchy :
Libertarian Philosophy
Quotes
War and Peace
: Skeptical
Finance : John
Kenneth Galbraith :Talleyrand :
Oscar Wilde :
Otto Von Bismarck :
Keynes :
George Carlin :
Skeptics :
Propaganda : SE
quotes : Language Design and Programming Quotes :
Random IT-related quotes :
Somerset Maugham :
Marcus Aurelius :
Kurt Vonnegut :
Eric Hoffer :
Winston Churchill :
Napoleon Bonaparte :
Ambrose Bierce :
Bernard Shaw :
Mark Twain Quotes
Bulletin:
Vol 25, No.12 (December, 2013) Rational Fools vs. Efficient Crooks The efficient
markets hypothesis :
Political Skeptic Bulletin, 2013 :
Unemployment Bulletin, 2010 :
Vol 23, No.10
(October, 2011) An observation about corporate security departments :
Slightly Skeptical Euromaydan Chronicles, June 2014 :
Greenspan legacy bulletin, 2008 :
Vol 25, No.10 (October, 2013) Cryptolocker Trojan
(Win32/Crilock.A) :
Vol 25, No.08 (August, 2013) Cloud providers
as intelligence collection hubs :
Financial Humor Bulletin, 2010 :
Inequality Bulletin, 2009 :
Financial Humor Bulletin, 2008 :
Copyleft Problems
Bulletin, 2004 :
Financial Humor Bulletin, 2011 :
Energy Bulletin, 2010 :
Malware Protection Bulletin, 2010 : Vol 26,
No.1 (January, 2013) Object-Oriented Cult :
Political Skeptic Bulletin, 2011 :
Vol 23, No.11 (November, 2011) Softpanorama classification
of sysadmin horror stories : Vol 25, No.05
(May, 2013) Corporate bullshit as a communication method :
Vol 25, No.06 (June, 2013) A Note on the Relationship of Brooks Law and Conway Law
History:
Fifty glorious years (1950-2000):
the triumph of the US computer engineering :
Donald Knuth : TAoCP
and its Influence of Computer Science : Richard Stallman
: Linus Torvalds :
Larry Wall :
John K. Ousterhout :
CTSS : Multix OS Unix
History : Unix shell history :
VI editor :
History of pipes concept :
Solaris : MS DOS
: Programming Languages History :
PL/1 : Simula 67 :
C :
History of GCC development :
Scripting Languages :
Perl history :
OS History : Mail :
DNS : SSH
: CPU Instruction Sets :
SPARC systems 1987-2006 :
Norton Commander :
Norton Utilities :
Norton Ghost :
Frontpage history :
Malware Defense History :
GNU Screen :
OSS early history
Classic books:
The Peter
Principle : Parkinson
Law : 1984 :
The Mythical Man-Month :
How to Solve It by George Polya :
The Art of Computer Programming :
The Elements of Programming Style :
The Unix Haterís Handbook :
The Jargon file :
The True Believer :
Programming Pearls :
The Good Soldier Svejk :
The Power Elite
Most popular humor pages:
Manifest of the Softpanorama IT Slacker Society :
Ten Commandments
of the IT Slackers Society : Computer Humor Collection
: BSD Logo Story :
The Cuckoo's Egg :
IT Slang : C++ Humor
: ARE YOU A BBS ADDICT? :
The Perl Purity Test :
Object oriented programmers of all nations
: Financial Humor :
Financial Humor Bulletin,
2008 : Financial
Humor Bulletin, 2010 : The Most Comprehensive Collection of Editor-related
Humor : Programming Language Humor :
Goldman Sachs related humor :
Greenspan humor : C Humor :
Scripting Humor :
Real Programmers Humor :
Web Humor : GPL-related Humor
: OFM Humor :
Politically Incorrect Humor :
IDS Humor :
"Linux Sucks" Humor : Russian
Musical Humor : Best Russian Programmer
Humor : Microsoft plans to buy Catholic Church
: Richard Stallman Related Humor :
Admin Humor : Perl-related
Humor : Linus Torvalds Related
humor : PseudoScience Related Humor :
Networking Humor :
Shell Humor :
Financial Humor Bulletin,
2011 : Financial
Humor Bulletin, 2012 :
Financial Humor Bulletin,
2013 : Java Humor : Software
Engineering Humor : Sun Solaris Related Humor :
Education Humor : IBM
Humor : Assembler-related Humor :
VIM Humor : Computer
Viruses Humor : Bright tomorrow is rescheduled
to a day after tomorrow : Classic Computer
Humor
The Last but not Least Technology is dominated by
two types of people: those who understand what they do not manage and those who manage what they do not understand ~Archibald Putt.
Ph.D
Copyright © 1996-2021 by Softpanorama Society. www.softpanorama.org
was initially created as a service to the (now defunct) UN Sustainable Development Networking Programme (SDNP)
without any remuneration. This document is an industrial compilation designed and created exclusively
for educational use and is distributed under the Softpanorama Content License.
Original materials copyright belong
to respective owners. Quotes are made for educational purposes only
in compliance with the fair use doctrine.
FAIR USE NOTICE This site contains
copyrighted material the use of which has not always been specifically
authorized by the copyright owner. We are making such material available
to advance understanding of computer science, IT technology, economic, scientific, and social
issues. We believe this constitutes a 'fair use' of any such
copyrighted material as provided by section 107 of the US Copyright Law according to which
such material can be distributed without profit exclusively for research and educational purposes.
This is a Spartan WHYFF (We Help You For Free)
site written by people for whom English is not a native language. Grammar and spelling errors should
be expected. The site contain some broken links as it develops like a living tree...
Disclaimer:
The statements, views and opinions presented on this web page are those of the author (or
referenced source) and are
not endorsed by, nor do they necessarily reflect, the opinions of the Softpanorama society. We do not warrant the correctness
of the information provided or its fitness for any purpose. The site uses AdSense so you need to be aware of Google privacy policy. You you do not want to be
tracked by Google please disable Javascript for this site. This site is perfectly usable without
Javascript.
Last modified: March, 12, 2019






