|
|
Home | Switchboard | Unix Administration | Red Hat | TCP/IP Networks | Neoliberalism | Toxic Managers |
| (slightly skeptical) Educational society promoting "Back to basics" movement against IT overcomplexity and bastardization of classic Unix | |||||||
|
|
Graph theory is the study of the properties of graphs. Graph algorithms are one of the oldest classes of algorithms and they have been studied for almost 300 years (in 1736 Leonard Euler formulated one of the first graph problems Königsberg Bridge Problem, see history).
|
|
There are two large classes of graphs:
Some algorithms differ by the class. Moreover the set of problems for digraphs and undirected graphs are different. There are special cases of digraphs and graphs that have thier own sets of problem. One example for digraphs will be program graphs. Program graphs are important in compiler construction and were studied in detail after the invention of the computers.
Graphs are made up of vertices and edges. The simplest property of a vertex is its degree,
the number of edges incident upon it. The sum of the vertex degrees in any undirected graph is twice
the number of edges, since every edge contributes one to the degree of both adjacent vertices. Trees
are undirected graphs which contain no cycles. Vertex degrees are important in the analysis of trees.
A leaf of a tree is a vertex of degree 1. Every
![]() -vertex tree contains
-vertex tree contains
![]() edges, so all
non-trivial trees contain at least two leaf vertices.
edges, so all
non-trivial trees contain at least two leaf vertices.
Among classic algorithms/problems on digraphs we can note the following:
Some differences between graphs lists and trees:
Here is a nice outline of typical problems at CSE 392 - Programming Challenges Graph Algorithms (Week 10)
|
|
Switchboard | ||||
| Latest | |||||
| Past week | |||||
| Past month | |||||
December 23, 2003 | Amazon.com
Mike Blaszczak on December 23, 2003
Intersting Studies Hampered by LEDA and LP DependenciesI'm pleased with the text in this book; the descriptions are almost all clear, and reading through the book gives me insight into some more interesting problems in trees and graphs. The high points of the book are its treaments of tree and graph isomorphism, but I also found the discussions of non-traditional traversal algorithms on trees and graphs very interesting. The author discussions leaf-first, breadth-first, and depth-first traversals and provides algorithms for their implementation. Many of the algorithms include correctness proofs.
These topics alone made the book worth its to me. A deep academic book that costs less than $50 is nearly unheared-of.Unfortunately, there are two flaws that make the book hard to use. In a nutshell, the author expects the reader to buy into a couple of pretty invasive and expensive propositions.
First, the author decided to use literate programming for all of his presented algorithms and code fragments. This isn't so bad, since literate programming is about documenting code. If you suppose that the author wrote the code, then documented it, then calld it a book, using a tool like literate programming seems like a natural choice.But if you're not familiar with literate programming, it's a bit of a chore. The author's introduction to literate programming doesn't help with some of the questions even an experienced programmer might have wend reading the text. More practically, literate programming enforces operators that are different than most C/C++ developers are familiar with, and can cause confusion when reading the text. ^ is used, for example, to indicate a logical and, where C/C++ developers expect it to indicate a bitwise-exclusive or.
While it's esay to eventually overcome such tricks of memory, I've been finding it hard to scan literate programs to find definitions and declarations. The author doesn't include a CD (and at this cover price, that is hard to fault) but also doesn't make his code available for download. His website includes a LEDA-based program that interactively demonstrates some algorithms, but doesn't include code for the algorithm his own books develops and discusses.
The other decision made by the author, to the overwhelming inconvenience of this reader, is the reliance on the LEDA library for his samples and programs. The algorithms are understandable without the library, but a reader without access to LEDA doesn't benefit from any of the visualizations the author provides. , and several include
In fact, the author spends about 40 pages discussing LEDA and the characteristics of its implementation. Maybe researchers working on tree and graph algorithms all use LEDA and have ready access to it, but the literate programming code provided to for some of the algorithms isn't useful to readers who aren't familiar with LEDA, as researching the definitions and declarations themsleves becomes arduous.
The bibliography is very diverse, with more than 380 entries and is well-cited throughout the book. Unfortunately, the author sometimes relies on the bibliography too much. On page 392, the author brings up "the so-called graph isopomorphism disease" without defining it himself; he instead relies on his bibliography entries to give the user any definition or background on the "disease".
Unfortunately, the index received not nearly as much attention as the bibliography; neglecting whitespace, it's scarcely more than a single page long!
The book appears to be something more than a research paper, but is written much like a research apper would be. The book probably also serves well for a class that teaches this subject, and assumes LEDA and literate programming as prerequisites. But as a commercial developer who's interested in applying advanced graph and tree algorithms to the work I'm doing, I found the book has limited its value by relying on LEDA and applying literate programming.
All this said, I still feel it's appropriate to give the book four stars. The material covered is hard to find elsewhere, and with some effort I can overcome the LEDA and literate programming hurdles. Since I don't use LEDA or literate programming day-to-day, I'll have to overcome that unfamiliarity every time I pick up the book as a reference.
Digital Puer on June 1, 2009
Book centered entirely on combinatorial subgraph problems
This book's title is very misleading, as the author's focus really is on subgraph problems (e.g. subgraph and tree isomorphism, clique, independent set, and vertex cover).The book barely mentions other graph theory topics such as distance algorithms (e.g. single-source shortest path, minimum-spanning tree, transitive closure), network flow, or graph colouring. This odd focus is really frustrating since the author spends a large number of pages on relatively simple topics such as tree traversal (34 pages on things like pre-order traversal) and graph traversal (42 pages on things like depth-first search). In fact, in section 5.3 on graph traversal applications, the author suggests that the reader may have already learned about algorithms such as shortest path or topological sorting, so he instead gives an example of ordered graph isomorphism. I do not understand why the author would make such an assumption; if the reader is assumed to already know about many applications of graph traversal, then why did the author spend 42 pages explaining what graph traversal is?
I believe one possible reason why the author does not discuss such "simpler" graph algorithms is that the LEDA library already has functions that implement algorithms like Dijkstra's, Bellman-Ford, MST, and max flow. However, the author does not spend time even defining what these problems are and only mentions the existence of these functions in the appendix.
Other things I did not like about the book:
- Much of the material seems to be simply cut-and-paste from one topic to the next. Case in point: the chunk of text saying "The problem of [problem] belongs to the class of NP-complete problems ... size of the graph" is pasted verbatim into at least four sections.Read more ›
Chenna Reddy Cotla on March 29, 2010
literate programming killed the bookGood on describing graph theory algorithms but is rendered bad due to that literate programming ... Simple algorithmic notation would have made the book much better...
Olga Kharitonova on July 13, 2014
The book has ridiculous price taking into account amount of content. Literate programming hams it it as well.
SGE Grid Job Dependency
It is possible to describe SGE (Sun Grid Engine) job (or any other grid engine) dependency in a DAG (Directed Acyclic Graph) format. By taking advantage of the opensource Graphviz, it is very easy to document this dependency in DOT language format. Below shows you a sample DOT file:$ cat job-dep.dot digraph jobs101 { job_1 -> job_11; job_1 -> job_12; job_1 -> job_13; job_11 -> job_111; job_12 -> job_111; job_2 -> job_13; job_2 -> job_21; job_3 -> job_21; job_3 -> job_31; }With this DOT file, one can generate the graphical representation:
$ dot -Tpng -o job-dep.png job-dep.dot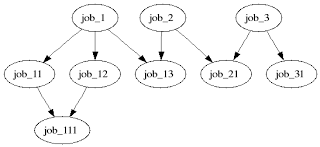
It is also possible to derive the corresponding SGE commands by the following Tcl script.
$ cat ./dot2sge.tcl #! /usr/local/bin/tclsh if { $argc != 1 } { puts stderr "Usage: $argv0" exit 1 } set dotfile [lindex $argv 0] if { [file exists $dotfile] == 0 } { puts stderr "Error. $dotfile does not exist" exit 2 } # assume simple directed graph a -> b set fp [open $dotfile r] set data [read $fp] close $fp set sge_jobs {} foreach i [split [lindex $data 2] {;}] { if { [regexp {(\w+)\s*->\s*(\w+)} $i x parent child] != 0 } { lappend sge_jobs $parent lappend sge_jobs $child lappend sge_job_rel($parent) $child } } # submit unique jobs, and hold set queue all.q set sge_unique_jobs [lsort -unique $sge_jobs] foreach i $sge_unique_jobs { puts "qsub -h -q $queue -N $i job-submit.sh" } # alter the job dependency, but unhold after all the hold relationships are # established foreach i $sge_unique_jobs { if { [info exists sge_job_rel($i)] } { # with dependency puts "qalter -hold_jid [join $sge_job_rel($i) {,}] $i" } } foreach i $sge_unique_jobs { puts "qalter -h U $i" } Run this Tcl script to generate the SGE submission commands and alternation commands to register the job dependency
$ ./dot2sge.tcl job-dep.dot qsub -h -q all.q -N job_1 job-submit.sh qsub -h -q all.q -N job_11 job-submit.sh qsub -h -q all.q -N job_111 job-submit.sh qsub -h -q all.q -N job_12 job-submit.sh qsub -h -q all.q -N job_13 job-submit.sh qsub -h -q all.q -N job_2 job-submit.sh qsub -h -q all.q -N job_21 job-submit.sh qsub -h -q all.q -N job_3 job-submit.sh qsub -h -q all.q -N job_31 job-submit.sh qalter -hold_jid job_11,job_12,job_13 job_1 qalter -hold_jid job_111 job_11 qalter -hold_jid job_111 job_12 qalter -hold_jid job_13,job_21 job_2 qalter -hold_jid job_21,job_31 job_3 qalter -h U job_1 qalter -h U job_11 qalter -h U job_111 qalter -h U job_12 qalter -h U job_13 qalter -h U job_2 qalter -h U job_21 qalter -h U job_3 qalter -h U job_31Below show the above proof-of-concept in action. So sit back....
# # ----------below is a very simple script # $ cat job-submit.sh #! /bin/sh #$ -S /bin/sh date sleep 10 # # ----------run all the qsub to submit jobs, but put them on hold # $ qsub -h -q all.q -N job_1 job-submit.sh Your job 333 ("job_1") has been submitted. $ qsub -h -q all.q -N job_11 job-submit.sh Your job 334 ("job_11") has been submitted. $ qsub -h -q all.q -N job_111 job-submit.sh Your job 335 ("job_111") has been submitted. $ qsub -h -q all.q -N job_12 job-submit.sh Your job 336 ("job_12") has been submitted. $ qsub -h -q all.q -N job_13 job-submit.sh Your job 337 ("job_13") has been submitted. $ qsub -h -q all.q -N job_2 job-submit.sh Your job 338 ("job_2") has been submitted. $ qsub -h -q all.q -N job_21 job-submit.sh Your job 339 ("job_21") has been submitted. $ qsub -h -q all.q -N job_3 job-submit.sh Your job 340 ("job_3") has been submitted. $ qsub -h -q all.q -N job_31 job-submit.sh Your job 341 ("job_31") has been submitted. # # ----------show the status, all jobs are in hold position (hqw) # $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 0/4 0.01 sol-amd64 ############################################################################ - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS ############################################################################ 333 0.00000 job_1 chihung hqw 07/19/2007 21:04:34 1 334 0.00000 job_11 chihung hqw 07/19/2007 21:04:34 1 335 0.00000 job_111 chihung hqw 07/19/2007 21:04:34 1 336 0.00000 job_12 chihung hqw 07/19/2007 21:04:34 1 337 0.00000 job_13 chihung hqw 07/19/2007 21:04:34 1 338 0.00000 job_2 chihung hqw 07/19/2007 21:04:34 1 339 0.00000 job_21 chihung hqw 07/19/2007 21:04:34 1 340 0.00000 job_3 chihung hqw 07/19/2007 21:04:34 1 341 0.00000 job_31 chihung hqw 07/19/2007 21:04:34 1 # # ----------register the job dependency # $ qalter -hold_jid job_11,job_12,job_13 job_1 modified job id hold list of job 333 blocking jobs: 334,336,337 exited jobs: NONE $ qalter -hold_jid job_111 job_11 modified job id hold list of job 334 blocking jobs: 335 exited jobs: NONE $ qalter -hold_jid job_111 job_12 modified job id hold list of job 336 blocking jobs: 335 exited jobs: NONE $ qalter -hold_jid job_13,job_21 job_2 modified job id hold list of job 338 blocking jobs: 337,339 exited jobs: NONE $ qalter -hold_jid job_21,job_31 job_3 modified job id hold list of job 340 blocking jobs: 339,341 exited jobs: NONE # # ----------release all the holds and let SGE to sort itself out # $ qalter -h U job_1 modified hold of job 333 $ qalter -h U job_11 modified hold of job 334 $ qalter -h U job_111 modified hold of job 335 $ qalter -h U job_12 modified hold of job 336 $ qalter -h U job_13 modified hold of job 337 $ qalter -h U job_2 modified hold of job 338 $ qalter -h U job_21 modified hold of job 339 $ qalter -h U job_3 modified hold of job 340 $ qalter -h U job_31 modified hold of job 341 # # ----------query SGE stats # $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 0/4 0.01 sol-amd64 ############################################################################ - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS ############################################################################ 333 0.00000 job_1 chihung hqw 07/19/2007 21:04:34 1 334 0.00000 job_11 chihung hqw 07/19/2007 21:04:34 1 335 0.00000 job_111 chihung qw 07/19/2007 21:04:34 1 336 0.00000 job_12 chihung hqw 07/19/2007 21:04:34 1 337 0.00000 job_13 chihung qw 07/19/2007 21:04:34 1 338 0.00000 job_2 chihung hqw 07/19/2007 21:04:34 1 339 0.00000 job_21 chihung qw 07/19/2007 21:04:34 1 340 0.00000 job_3 chihung hqw 07/19/2007 21:04:34 1 341 0.00000 job_31 chihung qw 07/19/2007 21:04:34 1 # # ----------some jobs started to run # $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 2/4 0.01 sol-amd64 339 0.55500 job_21 chihung r 07/19/2007 21:05:36 1 341 0.55500 job_31 chihung r 07/19/2007 21:05:36 1 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 1/4 0.01 sol-amd64 335 0.55500 job_111 chihung r 07/19/2007 21:05:36 1 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 1/4 0.01 sol-amd64 337 0.55500 job_13 chihung r 07/19/2007 21:05:36 1 ############################################################################ - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS ############################################################################ 333 0.00000 job_1 chihung hqw 07/19/2007 21:04:34 1 334 0.00000 job_11 chihung hqw 07/19/2007 21:04:34 1 336 0.00000 job_12 chihung hqw 07/19/2007 21:04:34 1 338 0.00000 job_2 chihung hqw 07/19/2007 21:04:34 1 340 0.00000 job_3 chihung hqw 07/19/2007 21:04:34 1 $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 2/4 0.01 sol-amd64 339 0.55500 job_21 chihung r 07/19/2007 21:05:36 1 341 0.55500 job_31 chihung r 07/19/2007 21:05:36 1 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 1/4 0.01 sol-amd64 335 0.55500 job_111 chihung r 07/19/2007 21:05:36 1 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 1/4 0.01 sol-amd64 337 0.55500 job_13 chihung r 07/19/2007 21:05:36 1 ############################################################################ - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS ############################################################################ 333 0.00000 job_1 chihung hqw 07/19/2007 21:04:34 1 334 0.00000 job_11 chihung hqw 07/19/2007 21:04:34 1 336 0.00000 job_12 chihung hqw 07/19/2007 21:04:34 1 338 0.00000 job_2 chihung hqw 07/19/2007 21:04:34 1 340 0.00000 job_3 chihung hqw 07/19/2007 21:04:34 1 $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 0/4 0.01 sol-amd64 ############################################################################ - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS ############################################################################ 333 0.00000 job_1 chihung hqw 07/19/2007 21:04:34 1 334 0.00000 job_11 chihung qw 07/19/2007 21:04:34 1 336 0.00000 job_12 chihung qw 07/19/2007 21:04:34 1 338 0.00000 job_2 chihung qw 07/19/2007 21:04:34 1 340 0.00000 job_3 chihung qw 07/19/2007 21:04:34 1 $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 2/4 0.01 sol-amd64 338 0.55500 job_2 chihung r 07/19/2007 21:05:51 1 340 0.55500 job_3 chihung r 07/19/2007 21:05:51 1 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 1/4 0.01 sol-amd64 334 0.55500 job_11 chihung r 07/19/2007 21:05:51 1 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 1/4 0.01 sol-amd64 336 0.55500 job_12 chihung r 07/19/2007 21:05:51 1 ############################################################################ - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS ############################################################################ 333 0.00000 job_1 chihung hqw 07/19/2007 21:04:34 1 $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 2/4 0.01 sol-amd64 338 0.55500 job_2 chihung r 07/19/2007 21:05:51 1 340 0.55500 job_3 chihung r 07/19/2007 21:05:51 1 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 1/4 0.01 sol-amd64 334 0.55500 job_11 chihung r 07/19/2007 21:05:51 1 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 1/4 0.01 sol-amd64 336 0.55500 job_12 chihung r 07/19/2007 21:05:51 1 ############################################################################ - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS ############################################################################ 333 0.00000 job_1 chihung hqw 07/19/2007 21:04:34 1 $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 0/4 0.01 sol-amd64 ############################################################################ - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS - PENDING JOBS ############################################################################ 333 0.00000 job_1 chihung qw 07/19/2007 21:04:34 1 $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 1/4 0.01 sol-amd64 333 0.55500 job_1 chihung r 07/19/2007 21:06:06 1 $ qstat -f queuename qtype used/tot. load_avg arch states ---------------------------------------------------------------------------- all.q@sgeexec0 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec1 BIP 0/4 0.01 sol-amd64 ---------------------------------------------------------------------------- all.q@sgeexec2 BIP 1/4 0.01 sol-amd64 333 0.55500 job_1 chihung r 07/19/2007 21:06:06 1 # # ----------output of all jobs, you can see job job_1/2/3 finished last # $ grep 2007 job_*.o* job_111.o335:Thu Jul 19 21:05:36 SGT 2007 job_11.o334:Thu Jul 19 21:05:51 SGT 2007 job_12.o336:Thu Jul 19 21:05:51 SGT 2007 job_13.o337:Thu Jul 19 21:05:36 SGT 2007 job_1.o333:Thu Jul 19 21:06:06 SGT 2007 job_21.o339:Thu Jul 19 21:05:36 SGT 2007 job_2.o338:Thu Jul 19 21:05:51 SGT 2007 job_31.o341:Thu Jul 19 21:05:37 SGT 2007 job_3.o340:Thu Jul 19 21:05:52 SGT 2007Another successful proof-of-concept. :-)
Learn about Apache Giraph, GraphLab, and other open source systems for processing graph-structured big data. More >
- There are three missionaries and three cannibals on the left bank of a river.
- They wish to cross over to the right bank using a boat that can only carry two at a time.
- The number of cannibals on either bank must never exceed the number of missionaries on the same bank, otherwise the missionaries will become the cannibals' dinner!
- Plan a sequence of crossings that will take everyone safely accross.
This kind of problem is often solved by a graph search method. We represent the problem as a set of
States can be mapped to nodes of a graph and operators are the edges of the graph. Before studying the missionaries and cannibals problem, we look at a simple graph search algorithm in Prolog. the missionaries and cannibals program will have the same basic structure.
- states
- which are snapshots of the world and
- operators
- which transform one state into another
Graph Representation
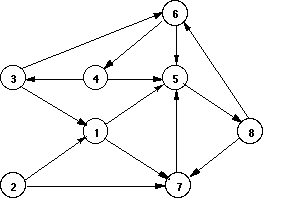
A graph may be represented by a set of edge predicates and a list of vertices.
edge(1, 5). edge(1, 7). edge(2, 1). edge(2, 7). edge(3, 1). edge(3, 6). edge(4, 3). edge(4, 5). edge(5, 8). edge(6, 4). edge(6, 5). edge(7, 5). edge(8, 6). edge(8, 7). vertices([1, 2, 3, 4, 5, 6, 7, 8]).
Finding a path
- Write a program to find path from one node to another.
- Must avoid cycles (i.e. going around in circle).
- A template for the clause is:
path(Start, Finish, Visited, Path).
- Start
- is the name of the starting node
- Finish
- is the name of the finishing node
- Visited
- is the list of nodes already visited.
- Path
- is the list of nodes on the path, including Start and Finish.
The Path Program
- The search for a path terminates when we have nowhere to go.
path(Node, Node, _, [Node]).
- A path from Start to Finish starts with a node, X, connected to Start followed by a path from X to Finish.
path(Start, Finish, Visited, [Start | Path]) :- edge(Start, X), not(member(X, Visited)), path(X, Finish, [X | Visited], Path).Here is an example of the path algorithm in action.Representing the state
Now we return to the problem of representing the missionaries anc cannibals problem:
- A state is one "snapshot" in time.
- For this problem, the only information we need to fully characterise the state is:
All other information can be deduced from these three items.
- the number of missionaries on the left bank,
- the number of cannibals on the left bank,
- the side the boat is on.
- In Prolog, the state can be represented by a 3-arity term,
state(Missionaries, Cannibals, Side)
Representing the Solution
- The solution consists of a list of moves, e.g.
[move(1, 1, right), move(2, 0, left)]
- We take this to mean that 1 missionary and 1 cannibal moved to the right bank, then 2 missinaries moved to the left bank.
- Like the graph search problem, we must avoid returning to a state we have visited before.
- The visited list will have the form:
[MostRecent_State | ListOfPreviousStates]Overview of Solution
- We follow a simple graph search procedure:
The search terminates whe we have found the state:
- Start from an initial state
- Find a neighbouring state
- Check that the new state has not been visited before
- Find a path from the neighbour to the goal.
state(0, 0, right).
Top-level Prolog Code
% mandc(CurrentState, Visited, Path) mandc(state(0, 0, right), _, []). mandc(CurrentState, Visited, [Move | RestOfMoves]) :- newstate(CurrentState, NextState), not(member(NextState, Visited)), make_move(CurrentState, NextState, Move), mandc(NextState, [NextState | Visited], RestOfMoves]). make_move(state(M1, C1, left), state(M2, C2, right), move(M, C, right)) :- M is M1 - M2, C is C1 - C2. make_move(state(M1, C1, right), state(M2, C2, left), move(M, C, left)) :- M is M2 - M1, C is C2 - C1.
Possible Moves
- A move is characterised by the number of missionaries and the number of cannibals taken in the boat at one time.
- Since the boat can carry no more than two people at once, the only possible combinations are:
carry(2, 0). carry(1, 0). carry(1, 1). carry(0, 1). carry(0, 2).
- where carry(M, C) means the boat will carry M missionaries and C cannibals on one trip.
Feasible Moves
- Once we have found a possible move, we have to confirm that it is feasible.
- I.e. it is not feasible to move more missionaries or more cannibals than are present on one bank.
- When the state is state(M1, C1, left) and we try carry(M, C) then
M <= M1 and C <= C1
- must be true.
- When the state is state(M1, C1, right) and we try carry(M, C) then
M + M1 <= 3 and C + C1 <= 3
- must be true.
Legal Moves
- Once we have found a feasible move, we must check that is legal.
- I.e. no missionaries must be eaten.
legal(X, X). legal(3, X). legal(0, X).
- The only safe combinations are when there are equal numbers of missionaries and cannibals or all the missionaries are on one side.
Generating the next state
newstate(state(M1, C1, left), state(M2, C2, right)) :- carry(M, C), M <= M1, C <= C1, M2 is M1 - M, C2 is C1 - C, legal(M2, C2). newstate(state(M1, C1, right), state(M2, C2, left)) :- carry(M, C), M2 is M1 + M, C2 is C1 + C, M2 <= 3, C2 <= 3, legal(M2, C2).The complete code, with instructions for use, is available at http://www.cse.unsw.edu.au/~billw/cs9414/notes/mandc/mandc.pro
Methods of Search
In the preceding example, the state space is explored in an order determined by Prolog. In some situations, it might be necessary to alter that order of search in order to make search more efficient. To see what this might mean, here are two alternative methods of searching a tree.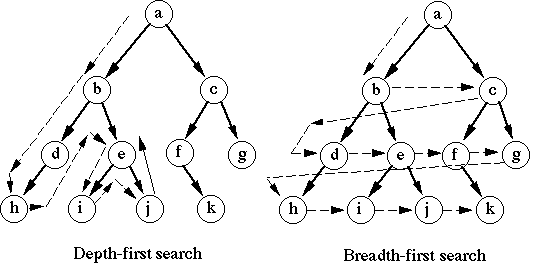
Depth first search begins by diving down as quickly as possible to the leaf nodes of the tree. Traversal can be done by:
- visiting the node first, then its children (pre-order traversal):
a b d h e i j c f k g - visiting the children first, then the node (post-order traversal):
h d i j e b k f g c a - visiting some of the children, then the node, then the other children (in-order traversal)
h d b i e j a f k c g There are many other search methods and variants on search methods. We do not have time to cover these in COMP9414, but you can find out about some of them in the text by Bratko. For example, chapter 12 deals with best-first search.
Consider the problem of finding connected components in a directed graph. Assume we have a node and we want to find all the nodes that are in the same connected component as the given node.
The first thought that comes to mind is: given a node X, find those nodes Y that are reachable from X and from which you can get back to X. So we will assume that edges are given by an
edge/2relation:sameSCC(X,Y) :- reach(X,Z), reach(Z,Y). :- table reach/2. reach(X,X). reach(X,Y) :- reach(X,Z), edge(Z,Y).Indeed given a node X, this will find all nodes in the same strongly connected component as X, however it will in general take O(n*e) time, where n is the number of nodes and e is the number of edges. The reason is that given an X, there are n possible Z values and for each of them, we will find everything reachable from them, and each search can take O(e) time.
However, we can do better. It is known that this problem can be solved in O(e) time. The idea is, given a node X, to find all nodes reachable from X following edges forward. Then find all nodes reachable from X following edges backward (i.e., follow edges against the arrow.) Then intersect the two sets. That will be the set of nodes in X's SCC, because if Y is in both these sets, you can follow the edges forward from X to Y and then since there is also a backwards path from X to Y, there is forward path from Y to X, so you can get from X to Y and back to X following edges forward. So the program that does this is:
% sameSCC(+X,-Y) sameSCC(X,Y) :- reachfor(X,Y), reachback(X,Y). :- table reachfor/2, reachback/2. reachfor(X,X). reachfor(X,Y) :- reachfor(X,Z),edge(Z,Y). reachback(X,X). reachback(X,Y) :- reachback(X,Z),edge(Y,Z).Let's now consider its complexity to see why it is O(e). For a fixed value X, the computation of the query
reachfor(X,Y)takes O(e) time. Then we may have O(n) calls toreachback(X,Y)(one for each Y) but they all use one underlying call toreachback(X,_)which takes O(e) and is done only once. So when we add all that up (assuming a connected graph), we get O(e) time.
Authors: Richard O'Keefe & Vitor Santos Costa
Implementation and documentation are copied from YAP 5.0.1. Thelibrary(ugraph)library is based on code originally written by Richard O'Keefe. The code was then extended to be compatible with the SICStus Prolog ugraphs library. Code and documentation have been cleaned and style has been changed to be more in line with the rest of SWI-Prolog.The ugraphs library was originally released in the public domain. YAP is convered by the Perl artistic license, which does not imply further restrictions on the SWI-Prolog LGPL license.
The routines assume directed graphs, undirected graphs may be implemented by using two edges.
Originally graphs where represented in two formats. The SICStus library and this version of
library(ugraphs.pl)only uses the S-representation. The S-representation of a graph is a list of (vertex-neighbors) pairs, where the pairs are in standard order (as produced by keysort) and the neighbors of each vertex are also in standard order (as produced by sort). This form is convenient for many calculations. Each vertex appears in the S-representation, also if it has no neighbors.
- vertices_edges_to_ugraph(+Vertices, +Edges, -Graph)
- Given a graph with a set of Vertices and a set of Edges, Graph must unify with the corresponding S-representation. Note that the vertices without edges will appear in Vertices but not in Edges. Moreover, it is sufficient for a vertice to appear in Edges.
?- vertices_edges_to_ugraph([],[1-3,2-4,4-5,1-5], L). L = [1-[3,5], 2-[4], 3-[], 4-[5], 5-[]]In this case all vertices are defined implicitly. The next example shows three unconnected vertices:
?- vertices_edges_to_ugraph([6,7,8],[1-3,2-4,4-5,1-5], L). L = [1-[3,5], 2-[4], 3-[], 4-[5], 5-[], 6-[], 7-[], 8-[]] ?- vertices(+Graph, -Vertices)
- Unify Vertices with all vertices appearing in graph Graph. Example:
?- vertices([1-[3,5],2-[4],3-[],4-[5],5-[]], L). L = [1, 2, 3, 4, 5]- edges(+Graph, -Edges)
- Unify Edges with all edges appearing in Graph. In the next example:
?- edges([1-[3,5],2-[4],3-[],4-[5],5-[]], L). L = [1-3, 1-5, 2-4, 4-5]- add_vertices(+Graph, +Vertices, -NewGraph)
- Unify NewGraph with a new graph obtained by adding the list of Vertices to the Graph. Example:
?- add_vertices([1-[3,5],2-[]], [0,1,2,9], NG). NG = [0-[], 1-[3,5], 2-[], 9-[]]- del_vertices(+Vertices, +Graph, -NewGraph)
- Unify NewGraph with a new graph obtained by deleting the list of Vertices and all the edges that start from or go to a vertex in Vertices to the Graph. Example:
?- del_vertices([2,1], [1-[3,5],2-[4],3-[],4-[5],5-[],6-[],7-[2,6],8-[]], NL). NL = [3-[],4-[5],5-[],6-[],7-[6],8-[]]- add_edges(+Graph, +Edges, -NewGraph)
- Unify NewGraph with a new graph obtained by adding the list of edges Edges to the graph Graph. Example:
?- add_edges([1-[3,5],2-[4],3-[],4-[5],5-[],6-[],7-[],8-[]], [1-6,2-3,3-2,5-7,3-2,4-5], NL). NL = [1-[3,5,6], 2-[3,4], 3-[2], 4-[5], 5-[7], 6-[], 7-[], 8-[]]- del_edges(+Graph, +Edges, -NewGraph)
- Unify NewGraph with a new graph obtained by removing the list of Edges from the Graph. Notice that no vertices are deleted. In the next example:
?- del_edges([1-[3,5],2-[4],3-[],4-[5],5-[],6-[],7-[],8-[]], [1-6,2-3,3-2,5-7,3-2,4-5,1-3], NL). NL = [1-[5],2-[4],3-[],4-[],5-[],6-[],7-[],8-[]]- transpose(+Graph, -NewGraph)
- Unify NewGraph with a new graph obtained from Graph by replacing all edges of the form V1-V2 by edges of the form V2-V1. The cost is O(|V|^2). Notice that an undirected graph is its own transpose. Example:
?- transpose([1-[3,5],2-[4],3-[],4-[5],5-[],6-[],7-[],8-[]], NL). NL = [1-[],2-[],3-[1],4-[2],5-[1,4],6-[],7-[],8-[]]- neighbours(+Vertex, +Graph, -Vertices)
- Unify Vertices with the list of neighbours of vertex Vertex in Graph. Example:
?- neighbours(4,[1-[3,5],2-[4],3-[], 4-[1,2,7,5],5-[],6-[],7-[],8-[]], NL). NL = [1,2,7,5]- neighbors(+Vertex, +Graph, -Vertices)
- American version of neighbours/3.
- complement(+Graph, -NewGraph)
- Unify NewGraph with the graph complementary to Graph. Example:
?- complement([1-[3,5],2-[4],3-[], 4-[1,2,7,5],5-[],6-[],7-[],8-[]], NL). NL = [1-[2,4,6,7,8],2-[1,3,5,6,7,8],3-[1,2,4,5,6,7,8], 4-[3,5,6,8],5-[1,2,3,4,6,7,8],6-[1,2,3,4,5,7,8], 7-[1,2,3,4,5,6,8],8-[1,2,3,4,5,6,7]]- compose(+LeftGraph, +RightGraph, -NewGraph)
- Compose, by connecting the drains of LeftGraph to the sources of RightGraph. Example:
?- compose([1-[2],2-[3]],[2-[4],3-[1,2,4]],L). L = [1-[4], 2-[1,2,4], 3-[]]- ugraph_union(+Graph1, +Graph2, -NewGraph)
- NewGraph is the union of Graph1 and Graph2. Example:
?- ugraph_union([1-[2],2-[3]],[2-[4],3-[1,2,4]],L). L = [1-[2], 2-[3,4], 3-[1,2,4]]- top_sort(+Graph, -Sort)
- Generate the set of nodes Sort as a topological sorting of graph Graph, if one is possible. A toplogical sort is possible if the graph is connected and acyclic. In the example we show how topological sorting works for a linear graph:
?- top_sort([1-[2], 2-[3], 3-[]], L). L = [1, 2, 3]- top_sort(+Graph, -Sort0, -Sort)
- Generate the difference list Sort-Sort0 as a topological sorting of graph Graph, if one is possible.
- transitive_closure(+Graph, -Closure)
- Generate the graph Closure as the transitive closure of graph Graph. Example:
?- transitive_closure([1-[2,3],2-[4,5],4-[6]],L). L = [1-[2,3,4,5,6], 2-[4,5,6], 4-[6]]- reachable(+Vertex, +Graph, -Vertices)
- Unify Vertices with the set of all vertices in graph Graph that are reachable from Vertex. Example:
?- reachable(1,[1-[3,5],2-[4],3-[],4-[5],5-[]],V). V = [1, 3, 5]
- Trees: Binary Tree Operations
- UGraphs: Graph and Digraph Operations
Unweighted Graph Operations
Directed and undirected graphs are fundamental data structures representing arbitrary relationships between data objects. This package provides a Prolog implementation of directed graphs, undirected graphs being a special case of directed graphs.
An unweighted directed graph (ugraph) is represented as a list of (vertex-neighbors) pairs, where the pairs are in standard order (as produced by
keysortwith unique keys) and the neighbors of each vertex are also in standard order (as produced bysort), every neighbor appears as a vertex even if it has no neighbors itself, and no vertex is a neighbor to itself.An undirected graph is represented as a directed graph where for each edge (U,V) there is a symmetric edge (V,U).
An edge (U,V) is represented as the term U-V. U and V must be distinct.
A vertex can be any term. Two vertices are distinct iff they are not identical (
==).A path from u to v is represented as a list of vertices, beginning with u and ending with v. A vertex cannot appear twice in a path. A path is maximal in a graph if it cannot be extended.
A tree is a tree-shaped directed graph (all vertices have a single predecessor, except the root node, which has none).
A strongly connected component of a graph is a maximal set of vertices where each vertex has a path in the graph to every other vertex.
Sets are represented as ordered lists (see Ordsets).
To load the package, enter the query
| ?- use_module(library(ugraphs)).The following predicates are defined for directed graphs.
vertices_edges_to_ugraph(+Vertices, +Edges, -Graph)- Is true if Vertices is a list of vertices, Edges is a list of edges, and Graph is a graph built from Vertices and Edges. Vertices and Edges may be in any order. The vertices mentioned in Edges do not have to occur explicitly in Vertices. Vertices may be used to specify vertices that are not connected by any edges.
vertices(+Graph, -Vertices)- Unifies Vertices with the vertices in Graph.
edges(+Graph, -Edges)- Unifies Edges with the edges in Graph.
add_vertices(+Graph1, +Vertices, -Graph2)- Graph2 is Graph1 with Vertices added to it.
del_vertices(+Graph1, +Vertices, -Graph2)- Graph2 is Graph1 with Vertices and all edges to and from them removed from it.
add_edges(+Graph1, +Edges, -Graph2)- Graph2 is Graph1 with Edges and their "to" and "from" vertices added to it.
del_edges(+Graph1, +Edges, -Graph2)- Graph2 is Graph1 with Edges removed from it.
transpose(+Graph, -Transpose)- Transpose is the graph computed by replacing each edge (u,v) in Graph by its symmetric edge (v,u). Takes O(N^2) time.
neighbors(+Vertex, +Graph, -Neighbors)neighbours(+Vertex, +Graph, -Neighbors)- Vertex is a vertex in Graph and Neighbors are its neighbors.
complement(+Graph, -Complement)- Complement is the complement graph of Graph, i.e. the graph that has the same vertices as Graph but only the edges that are not in Graph.
compose(+G1, +G2, -Composition)- Computes Composition as the composition of two graphs, which need not have the same set of vertices.
transitive_closure(+Graph, -Closure)- Computes Closure as the transitive closure of Graph in O(N^3) time.
symmetric_closure(+Graph, -Closure)- Computes Closure as the symmetric closure of Graph, i.e. for each edge (u,v) in Graph, add its symmetric edge (v,u). Takes O(N^2) time. This is useful for making a directed graph undirected.
top_sort(+Graph, -Sorted)- Finds a topological ordering of a Graph and returns the ordering as a list of Sorted vertices. Fails iff no ordering exists, i.e. iff the graph contains cycles. Takes O(N^2) time.
max_path(+V1, +V2, +Graph, -Path, -Cost)- Path is a longest path of cost Cost from V1 to V2 in Graph, there being no cyclic paths from V1 to V2. Takes O(N^2) time.
min_path(+V1, +V2, +Graph, -Path, -Cost)- Path is a shortest path of cost Cost from V1 to V2 in Graph. Takes O(N^2) time.
min_paths(+Vertex, +Graph, -Tree)- Tree is a tree of all the shortest paths from Vertex to every other vertex in Graph. This is the single-source shortest paths problem.
path(+Vertex, +Graph, -Path)- Given a Graph and a Vertex of Graph, returns a maximal Path rooted at Vertex, enumerating more paths on backtracking.
reduce(+Graph, -Reduced)- Reduced is the reduced graph for Graph. The vertices of the reduced graph are the strongly connected components of Graph. There is an edge in Reduced from u to v iff there is an edge in Graph from one of the vertices in u to one of the vertices in v.
reachable(+Vertex, +Graph, -Reachable)- Given a Graph and a Vertex of Graph, returns the set of vertices that are reachable from that Vertex, including Vertex itself. Takes O(N^2) time.
random_ugraph(+P, +N, -Graph)- Where P is a probability, unifies Graph with a random graph of vertices 1..N where each possible edge is included with probability P.
The following predicates are defined for undirected graphs only.
min_tree(+Graph, -Tree, -Cost)- Tree is a spanning tree of Graph with cost Cost, if it exists.
clique(+Graph, +K, -Clique)- Clique is a maximal clique (complete subgraph) of n vertices of Graph, where n \geq K. n is not necessarily maximal.
independent_set(+Graph, +K, -Set)- Set is a maximal independent (unconnected) set of n vertices of Graph, where n \geq K. n is not necessarily maximal.
coloring(+Graph, +K, -Coloring)colouring(+Graph, +K, -Coloring)- Coloring is a mapping from vertices to colors [1,n] of Graph such that all edges have distinct end colors, where n \leq K. The mapping is represented as an ordered list of Vertex-Color pairs. n is not necessarily minimal.
- WGraphs: Weighted Graph and Digraph Operations
File Format: PDF/Adobe Acrobat - View as HTML
The Dominator Graph. Lemma 4:. The dominators of a node form a chain. ... Finding Dominators in A Flow Graph. Input : A flow graph G = (N, As). ...
www.cs.uiuc.edu/class/sp06/ cs526/Notes/3controlflow.4up.pdf - Similar pages
File Format: Adobe PostScript - View as HTML
A simple and optimal algorithm for finding immediate dominators inreducible graphs. Technical Report D-261/96, TOPPS Bibliography, 1996. ...
www.research.ibm.com/people/r/rama/Papers/pldi00.ps Similar pages
The subject we now call graph theory, and perhaps the wider topic of topology, was founded on the work of Leonhard Euler, and a single famous problem called the Seven Bridges problem. Probably the first paper on graph theory was by Euler. In 1736 he wrote Solutio problematis ad geometriam situs pertinentis, Commetarii Academiae Scientiarum Imperialis Petropolitanae which translates into English as "The solution of a problem relating to the geometry of position." Euler was one of the first to expand geometry into problems that were independent of measurement. In the paper Euler discusses what was then a trendy local topic, whether or not it is possible to stroll around Konigsberg (now called Kaliningrad) crossing each of its bridges across the Pregel River exactly once. Euler generalized the problem and gave conditions which would solve any such stroll. You can see a map of the actual seven bridges of Konigsberg at this site at St. Andrews Univ.
The development of graph theory is very similar the development of probability theory, where much of the original work was motivated by efforts to understand games of chance. The large portions of graph theory have been motivated by the study of games and recreational mathematics. Generally speaking, we use graphs in two situations. Firstly, since a graph is a very convenient and natural way of representing the relationships between objects we represent objects by vertices and the relationship between them by lines. In many situations (problems) such a pictorial representation may be all that is needed. Example of such applications are chemical molecule and map coloring as shown in the diagrams below. Other examples are signal-flow graphs, Konigsberg bridges, tracing maze etc.
For a plane digraph the kernel number is the minimum number of faces to be deleted (i.e., the vertices of the boundary) such that the remaining digraph has a kernel. We show that determining whether the kernel number is at most some constant $k$ is NP-complete for every $k\geq 0$.
We consider the problem of computing a minimum cycle basis of a directed graph with m arcs and n nodes. We adapt the greedy approach proposed by Horton and hereby obtain a very simple exact algorithm of complexity O(m4n), being as fast as the first algorithm proposed for this problem. Moreover, the speed-up of Golynski and Horton applies to this problem, providing an exact algorithm of complexity O(mωn), in particular O(m3.376n). Finally, we prove that these greedy approaches fail for more specialized subclasses of directed cycle bases.
We consider s,t-flow problems in connected graphs with the additional requirement that one can decompose the flow into at most k paths for a given number k. Such flows are called k-splittable flows. In the multi-commodity case they generalize unsplittable flows. In this paper, we consider the problem MkSF, which means to find a maximum k-splittable s,t-flow. We show complexity and approximability results for this problem depending on k. Results work for directed and undirected graphs. Firstly, we show that for all constant integer k > 1 MkSF is strongly NP-hard and cannot be approximated with a guarantee better than 5/6. This is the first constant bound for the non-approximability of this problem. Secondly, we study MkSF with k depending on m, the number of edges, and n, the number of nodes of the graph. We prove that MkSF is NP-hard for 2 <= k <= m-n+1. We show that it is polynomially solvable for k >= m-n+2. Thus, there is no gap in the analysis. For the special case of simple graphs we show that MkSF is polynomially solvable for k = m - c for each integer constant c. That also holds for k=m-(log log p(m,n))^eps for every polynom p in n and m, eps in (0,1). It is well known that every flow in a graph can be decomposed into at most m paths and cycles. We show as a general result that the number of paths in such a decomposition can always be limited to m - n + 2.
....the fully dynamic single source shortest paths problem in digraphs with positive real arc weights. We are not aware of any experimental study in the case of arbitrary arc weights. On the other hand, several papers report on experimental works concerning different dynamic graph problems (see e.g. [2, 3, 11]) In this paper we make a step toward this direction and we present the first experimental study of the fully dynamic single source shortest paths problem in digraphs with arbitrary (negative and non negative) arc weights. We implemented and experimented several algorithms for updating shortest ....
G. Amato, G. Cattaneo, and G. F. Italiano. Experimental analysis of dynamic minimum spanning tree algorithms. In ACM-SIAM Symp. on Discrete Algorithms, pp. 1--10, 1997.
These lecture notes contain the reference material on graph algorithms for the course: Algorithms and Data Structures (415.220FT) and are based on Dr Michael Dinneen's lecture notes of the course 415.220SC given in 1999. Topics include computer representations (adjacency matrices and lists), graph searching (BFS and DFS), and basic graph algorithms such as computing the shortest distances between vertices and finding the (strongly) connected components.
Google matched content |
Shortest Path Problem Web Pages
GDR A Visualization Tool for Graph Algorithms
GraphEd -- Graph Editor and Layout Program
Maximal Common Subgraph (MCS) algorithm
Transitive Closure of a Graph - Warshall's Algorithm
Transitive closure algorithms based on graph traversal
[PDF] Digraphs Outline and Reading Digraphs Directed DFS Transitive ...
Efficient transitive closure computation in large digraphs
... components. The representation generalizes a previous method for compressing
the transitive closure of an acyclic graph. The new ...
1.4.5 Transitive Closure and Reduction
Find Transitive Closure of Parent-Child Relationship in Oracle9i
Boost Graph Library: Transitive Closure
Citebase - Mantaining Dynamic Matrices for Fully Dynamic ...
PPT] Chapter 9: More Graph Algorithms
Transitive Closure -- from MathWorld
Transitive Closure and Reduction
LEDA Guide- Transitive Closure and Transitive Reduction
Joseph Culberson's Graph Coloring Resources Page
LEDA moved to Algorithmic Solutions Software GmbH
LEDA Combinatorial and Graph Algorithms
The Stony Brook Algorithm Repository
Pearson Books - Boost Graph Library, The
"Euler's proof of the nonexistence of a so-called Eulerian (i.e., closed) path across all seven bridges of Königsberg, now known as the Königsberg bridge problem, is a famous precursor to graph theory. In fact, the study of various sorts of paths in graphs (e.g., Euler paths, Eulerian circuits, Hamiltonian paths, and Hamiltonian circuits) has many applications in real-world problems." (Eric W. Weisstein. "Graph." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Graph.html ) See also Wilson, Robin J.: "200 years of graph theory---a guided tour" Theory and applications of graphs (Proc. Internat. Conf., Western Mich. Univ., Kalamazoo, Mich., 1976), pp. 1--9. Lecture Notes in Math., Vol. 642, Springer, Berlin, 1978. MR58 #15981.
A longer version appeared in book form: Biggs, Norman L.; Lloyd, E. Keith; Wilson, Robin J.: "Graph theory: 1736--1936" Clarendon Press, Oxford, 1976. 239 pp. MR56#2771
Seven Bridges of Königsberg - Wikipedia, the free encyclopedia
Department of Mathematics The Bridges of Konigsburg
Königsburg was founded by the Teutonic Knights in 1255 at the meeting point of two branches of the river Pregel, and went on to be the capital of Prussia. It was flattened by bombing raids during the Second World War, and was annexed by the Soviet Union in 1945, at which stage it was renamed Kaliningrad. Today, it is in the small Russian parcel of land on the Baltic Sea that is wedged between Lithuania and Northeastern Poland.Many famous figures in history were born in Königsburg, including the philosopher Immanuel Kant, the mathematicians Christian Goldbach and David Hilbert, and the physicist Gustav Kirchhoff. To mathematicians, though, Königsburg is best known for a puzzle associated with its seven bridges (shown in blue on the map): its citizens pondered for a long time whether it was possible to walk about the city in such a way that you cross all seven bridges over the river Pregel exactly once.
This might seem like a fun but inconsequential problem. However it was the inspiration for a 1736 paper by the great Swiss mathematician Leonhard Euler (1707-1783) which arguably began the field of topology. In this paper, Euler proved that there was no such path around the city. In fact Euler gives a simple criterion which determines whether or not there is a solution to any similar problem with any number of bridges connecting any number of landmasses!
Euler first simplified the problem, replacing each landmass by a vertex (yellow dot) and each bridge by an arc (black path). Such a configuration of vertices and connecting arcs is nowadays known as a graph. The original problem is equivalent to the problem of travelling around the graph in such a way that you cross each arc exactly once. Defining the degree of a vertex to be the number of arcs that lead to it, Euler proved:
Theorem There exists a (at least one) path on a graph which travels along each arc exactly once if and only if the graph has at most two vertices of odd degree.
Königsberg Bridge Problem -- From MathWorld
Graphs History - Graphs Information
Graph theory had its origins in a seminal 1736 contribution of the famous Swiss mathematician Leonhard Euler, who was then living in Germany. In Königsberg, Germany, the Pregel river ran through the city such that in its center was an island, and after passing the island, the river broke into two parts. Seven bridges were built so that the people of the city could get from one part to another. People who lived in the area wondered whether it was possible to traverse each of the bridges exactly once and return to one's starting point. This remained an open question for many years; no one had been able to show how to do it, but none had a proof that it wasn't possible, either. Euler's analysis came up with the answer, which was in the negative.Euler's insight was in reducing the concrete problem of the bridges over the Pregel at Königsberg into an abstract representation using a graph. He considered that the situation of the bridges could be abstracted to a graph having four points connected in a certain way with seven edges. He then had to analyze whether it was possible to traverse the edges of the graph once each, so as to return to the point from whence one began. Such a path is now called, in his honor, an Eulerian path, and the criterion he evolved for the existence of such a path in a graph allowed for a simple proof to show why it was not possible to solve the Königsberg Bridge Problem, which is now given as an introduction to most graph theory texts.
After the solution to this problem by Euler, the study of graph theory was strangely relegated to the back burner for over two hundred years, but the period after the second world war saw a great increase in interest, motivated to a great extent by the rapid pace of research in the sciences, as well as the needs of the industry.
The origin of graph theory can be traced back to Euler's work on the Konigsberg bridges problem (1735), which subsequently led to the concept of an Eulerian graph. The study of cycles on polyhedra by the Thomas P. Kirkman (1806 - 95) and William R. Hamilton (1805-65) led to the concept of a Hamiltonian graph.
The concept of a tree, a connected graph without cycles, appeared implicitly in the work of Gustav Kirchhoff (1824-87), who employed graph-theoretical ideas in the calculation of currents in electrical networks or circuits. Later, Arthur Cayley (1821-95), James J. Sylvester(1806-97), George Polya(1887-1985), and others use 'tree' to enumerate chemical molecules.
The study of planar graphs originated in two recreational problems involving the complete graph K5 and the complete bipartite graph K3,3. These graphs proved to be planarity, as was subsequently demonstrated by Kuratowski. First problem was presented by A. F. Mobius around the year 1840 as follows
Once upon a time, there was a king with five sons.
In his will he stated that after his death the sons
should divide the kingdom into five provinces so
that the boundary of each province should have
a frontiers line in common with each of the other
four provinces.Here the problem is whether one can draw five mutually neighboring regions in the plane.
The king further stated that all five brothers should
join the provincial capital by roads so that no two
roads intersect.
Here the problem is that deciding whether the graph K5 is planar.
The origin of second problem is unknown but it is first mentioned by H. Dudeney in 1913 in its present form.
The puzzle is to lay a water, gas, and electricity
to each of the three houses without any pipe
crossing another.
This problem is that of deciding whether the graph K3,3 is planar.
The celebrated four-color problem was first posed by Francis Guthrie in 1852. and a celebrated incorrect "proof" by appeared in 1879 by Alfred B. Kempe. It was proved by Kenneth Appel and Wolfgang Haken in 1976 and a simpler and more systematic proof was produced by Neil Roberton, Daniel Sanders, Paul Seymour, and Robin Thomas in 1994.
THE GRAPH THEORY HYMN
Text by BOHDAN ZELINKA
Music by ZDENĔK RYJÁČEK
English text by DONALD A. PREECE1.
Seven bridges spanned the River Pregel,
Many more than might have been expected;
Königsberg's wise leaders were delighted
To have built such very splendid structures.2.
Crowds each ev'ning surged towards the river,
People walked bemused across the bridges,
Pondering a simple-sounding challenge
Which defeated them and left them puzzled.3.
Here's the problem; see if you can solve it!
Try it out at home an scraps of paper!
STARTING OUT AND ENDING AT THE SAME SPOT,
YOU MUST CROSS EACH BRIDGE JUST ONCE EACH EV'NING.Refrain:
Eulerian graphs all have this restriction:
THE DEGREE OF ANY POINT IS EVEN.
That's the oldest graph result
That mankind has ever known.4.
All the folk in Königsberg were frantic!
All their efforts ended up in failure!
Happily, a learn-ed math'matician
Had his house right there within the city.5.
Euler's mind was equal to the problem:
"Ah", he said, "You're bound to be disheartened.
Crossing each bridge only once per outing
Can't be done, I truly do assure you."Refrain:
Eulerian graphs …6.
Laws of Nature never can be altered,
We can'd change them, even if we wish to.
Nor can flooded rivers or great bridges
Interfere with scientific progress.7.
War brought strife and ruin to the Pregel;
Bombs destroyed those seven splendid bridges.
Euler's name and fame will, notwithstanding,
Be recalled with Königsberg's for ever.Refrain:
Eulerian graphs …8.
Thanks to Euler, Graph Theory is thriving.
Year by year it flourishes and blossoms,
Fertilising much of mathematics
And so rich in all its applications.9.
Colleagues, let us fill up all our glasses!
Colleagues, let us raise them now to toast the
Greatness and the everlasting glory
Of our Graph Theory, which we love dearly!
static boolean pathBetween(Object A, Object B) {
// Base case
if (A.equals(B)) return true;
// Recursive case
for(Iterator Cs = nextNodes(A); Cs.hasMoreElements(); ) {
C = Cs.nextElement();
if pathBetween(C,B) return true;
}
return false;
} // reachable
+----+ | | v | A -> C -> D -> B
Is there a path from A to B?
Is B equal to A? No.
Pick some neighbor of A. C is the only one.
Is there a path from C to B?
Is B equal to C? No.
Pick some neighbor of C. Let's pick A.
Is there a path from A to B?
Is B equal to A? No.
Pick some neighbor of A. C is the only one.
Is there a path form C to B?
...
static boolean pathBetween(Object A, Object B) {
// Note that we've seen the current node.
mark(A);
// Base case
if (A.equals(B)) return true;
// Recursive case
for(Iterator Cs = nextNodes(A); Cs.hasMoreElements(); ) {
C = Cs.nextElement();
if (!marked(C) && pathBetween(C,B)) return true;
}
return false;
} // reachable
Society
Groupthink : Two Party System as Polyarchy : Corruption of Regulators : Bureaucracies : Understanding Micromanagers and Control Freaks : Toxic Managers : Harvard Mafia : Diplomatic Communication : Surviving a Bad Performance Review : Insufficient Retirement Funds as Immanent Problem of Neoliberal Regime : PseudoScience : Who Rules America : Neoliberalism : The Iron Law of Oligarchy : Libertarian Philosophy
Quotes
War and Peace : Skeptical Finance : John Kenneth Galbraith :Talleyrand : Oscar Wilde : Otto Von Bismarck : Keynes : George Carlin : Skeptics : Propaganda : SE quotes : Language Design and Programming Quotes : Random IT-related quotes : Somerset Maugham : Marcus Aurelius : Kurt Vonnegut : Eric Hoffer : Winston Churchill : Napoleon Bonaparte : Ambrose Bierce : Bernard Shaw : Mark Twain Quotes
Bulletin:
Vol 25, No.12 (December, 2013) Rational Fools vs. Efficient Crooks The efficient markets hypothesis : Political Skeptic Bulletin, 2013 : Unemployment Bulletin, 2010 : Vol 23, No.10 (October, 2011) An observation about corporate security departments : Slightly Skeptical Euromaydan Chronicles, June 2014 : Greenspan legacy bulletin, 2008 : Vol 25, No.10 (October, 2013) Cryptolocker Trojan (Win32/Crilock.A) : Vol 25, No.08 (August, 2013) Cloud providers as intelligence collection hubs : Financial Humor Bulletin, 2010 : Inequality Bulletin, 2009 : Financial Humor Bulletin, 2008 : Copyleft Problems Bulletin, 2004 : Financial Humor Bulletin, 2011 : Energy Bulletin, 2010 : Malware Protection Bulletin, 2010 : Vol 26, No.1 (January, 2013) Object-Oriented Cult : Political Skeptic Bulletin, 2011 : Vol 23, No.11 (November, 2011) Softpanorama classification of sysadmin horror stories : Vol 25, No.05 (May, 2013) Corporate bullshit as a communication method : Vol 25, No.06 (June, 2013) A Note on the Relationship of Brooks Law and Conway Law
History:
Fifty glorious years (1950-2000): the triumph of the US computer engineering : Donald Knuth : TAoCP and its Influence of Computer Science : Richard Stallman : Linus Torvalds : Larry Wall : John K. Ousterhout : CTSS : Multix OS Unix History : Unix shell history : VI editor : History of pipes concept : Solaris : MS DOS : Programming Languages History : PL/1 : Simula 67 : C : History of GCC development : Scripting Languages : Perl history : OS History : Mail : DNS : SSH : CPU Instruction Sets : SPARC systems 1987-2006 : Norton Commander : Norton Utilities : Norton Ghost : Frontpage history : Malware Defense History : GNU Screen : OSS early history
Classic books:
The Peter Principle : Parkinson Law : 1984 : The Mythical Man-Month : How to Solve It by George Polya : The Art of Computer Programming : The Elements of Programming Style : The Unix Hater’s Handbook : The Jargon file : The True Believer : Programming Pearls : The Good Soldier Svejk : The Power Elite
Most popular humor pages:
Manifest of the Softpanorama IT Slacker Society : Ten Commandments of the IT Slackers Society : Computer Humor Collection : BSD Logo Story : The Cuckoo's Egg : IT Slang : C++ Humor : ARE YOU A BBS ADDICT? : The Perl Purity Test : Object oriented programmers of all nations : Financial Humor : Financial Humor Bulletin, 2008 : Financial Humor Bulletin, 2010 : The Most Comprehensive Collection of Editor-related Humor : Programming Language Humor : Goldman Sachs related humor : Greenspan humor : C Humor : Scripting Humor : Real Programmers Humor : Web Humor : GPL-related Humor : OFM Humor : Politically Incorrect Humor : IDS Humor : "Linux Sucks" Humor : Russian Musical Humor : Best Russian Programmer Humor : Microsoft plans to buy Catholic Church : Richard Stallman Related Humor : Admin Humor : Perl-related Humor : Linus Torvalds Related humor : PseudoScience Related Humor : Networking Humor : Shell Humor : Financial Humor Bulletin, 2011 : Financial Humor Bulletin, 2012 : Financial Humor Bulletin, 2013 : Java Humor : Software Engineering Humor : Sun Solaris Related Humor : Education Humor : IBM Humor : Assembler-related Humor : VIM Humor : Computer Viruses Humor : Bright tomorrow is rescheduled to a day after tomorrow : Classic Computer Humor
The Last but not Least Technology is dominated by two types of people: those who understand what they do not manage and those who manage what they do not understand ~Archibald Putt. Ph.D
Copyright © 1996-2021 by Softpanorama Society. www.softpanorama.org was initially created as a service to the (now defunct) UN Sustainable Development Networking Programme (SDNP) without any remuneration. This document is an industrial compilation designed and created exclusively for educational use and is distributed under the Softpanorama Content License. Original materials copyright belong to respective owners. Quotes are made for educational purposes only in compliance with the fair use doctrine.
FAIR USE NOTICE This site contains copyrighted material the use of which has not always been specifically authorized by the copyright owner. We are making such material available to advance understanding of computer science, IT technology, economic, scientific, and social issues. We believe this constitutes a 'fair use' of any such copyrighted material as provided by section 107 of the US Copyright Law according to which such material can be distributed without profit exclusively for research and educational purposes.
This is a Spartan WHYFF (We Help You For Free) site written by people for whom English is not a native language. Grammar and spelling errors should be expected. The site contain some broken links as it develops like a living tree...
|
|
You can use PayPal to to buy a cup of coffee for authors of this site |
Disclaimer:
The statements, views and opinions presented on this web page are those of the author (or referenced source) and are not endorsed by, nor do they necessarily reflect, the opinions of the Softpanorama society. We do not warrant the correctness of the information provided or its fitness for any purpose. The site uses AdSense so you need to be aware of Google privacy policy. You you do not want to be tracked by Google please disable Javascript for this site. This site is perfectly usable without Javascript.
Last modified: December 26, 2017