|
|
Home | Switchboard | Unix Administration | Red Hat | TCP/IP Networks | Neoliberalism | Toxic Managers |
| (slightly skeptical) Educational society promoting "Back to basics" movement against IT overcomplexity and bastardization of classic Unix | |||||||
| See Also | Recommended Books | Recommended Links | Recommended Papers | Donald Knuth | |
| Animations | Test suits | Reference | Presentations | Humor | Etc |
|
|
Heapsort is a really cool sorting algorithm, but it is pretty difficult to understand. Wikipedia has both skeleton algorithms and animation so this page is just a notes to the Wikipedia page.
First of all heapsort has an extremely important advantage over quicksort of worst-case O(n log n) runtime while being an in-place algorithm. Unfortunatly heapsort is not a stable sort. Mergesort is a stable sorting algorithms with the the same time bounds, but requires Ω(n) auxiliary space, whereas heapsort requires only a constant amount.
|
|
Heapsort works reasonably well for the most practically important cases of sorted and almost sorted arrays (quicksort requires O(n2) comparisons in worst case).
Heapsort does not have a locality of reference. On modern computers with large cache mergesort has several advantages over heapsort:The key notion used in heapsort is concept of heap. The latter is a binary tree represented as array in a non trivial way invented by Floyd. Tree represented without using pointers !
In heap each node has a value greater than both its children (if any). Each node in the heap corresponds to an element of the array, with the root node corresponding to the element with index 0 in the array. Heaptree has important property which actually makes it possible to be represented in memory as an array: for a node corresponding to index i, its left child has index (2*i + 1) and its right child has index (2*i + 2). There is a Wikipedia article covering heap Heap (data structure) but it is pretty uninformative as for implementation.
Heap is pretty counterintuitive data structure, very difficult to understand. A rare good explanation can be found at Heap Sort that we will follow with some modifications. There are three key properties of heap:
Left child can be found as 2i. Computing 2i is very fast and does not involves multiplication (which is pretty expensive operation). You just shift of binary representation of the index to the left one bit.
There are two additional derived properties:
All the levels of the tree are completely filled except possibly for the lowest level, which is filled from the left up to a point (in other words the tree is left complete)
All leaves are on, at most, two adjacent levels.
If any elements do not exist in the array, then the corresponding child node does not exist either.
Here is an example of the heap:
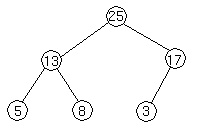
This heap is represented by the array A containing [25,13,17,5,8,3]. No let's check some properties that we outlined above.
The first element, 25, is clearly the root of the heap as, according to property 1, the sequence of operations floor(i/2) eventually gives you 1. Now the left child is A[2*1]=A[2]. As we see A[2]=13 and this is a child that we see on the picture. Similarly right child is A[3].
For A[2] children will be A[4] and A[5]. And for A[3] -- A[6] and A[7]. As we see A[3] does not have right child, as our array contains only 6 elements.
You can imagine heap as an idealized model of a tennis tournament result chart. The top guy that occupy the number one slot is the winner of the tournament. After him are two players who won the second and third place (note that the second place winner is not necessary occupy the left branch of the heap). Below the guy who won the second place are two guys he defeated on his way to the top, although they might be stronger that the guy who won the third place. You get the idea. So organizing the heap is very similar of conducting tennis tournament among the elements.
Note that in a heap the largest element is located at the root node. Heap Sort operates by first converting the initial array into a heap. The procedure used for this purpose traditionally is called heapify. In Wikipedia they substructure it into heapify and subroutine called siftUp although the latter is not strictly necessary and can be implemented inline (called only once from heapify). As you can see siftUp somewhat resembles bubblesort of non-sequential elements.
function heapify(a,count) is
(end is assigned the index of the first (left) child of the root)
end := 1
while end < count
(sift up the node at index end to the proper place such that all nodes above
the end index are in heap order)
siftUp(a, 0, end)
end := end + 1
(after sifting up the last node all nodes are in heap order)
function siftUp(a, start, end) is
input: start represents the limit of how far up the heap to sift.
end is the node to sift up.
child := end
while child > start
parent := floor((child - 1) ÷ 2)
if a[parent] < a[child] then (out of max-heap order)
swap(a[parent], a[child])
child := parent (repeat to continue sifting up the parent now)
else
return
The Heapify algorithm, as shown above, receives an array as input and arranges "tournament" between elements that are positioned in position N and floor(N/2). The "Winner" moved to lower position in the array (position floor(N/2)). The algorithm starts with element A[0] which is added to the heap. Then "games" are played between A[0] and A[1] and A[2] and each time the winner is swapped with the first position (A[0]). At this point A[0] represents the winner of mini-tournament consisting of three players A[0], A[1] and A[2].
Now we add another two elements A[3] and A[4] and conduct tournament between A[1], A[3] and A[4]. If any of then wins they are swapped with A[1] and additional "game" is played between A[0] and A[1] to determine the winner. In other words the element is sifted all way to its proper position in subsequence A[0], A[1] in a process the reminds bublesort.
After that we add elements A[4] and A[5] and the tournament is played between A[2], A[4] and A[5] in a similar way. Here element is sifted to its proper position in a sequence A[0], A[2]. Note that neither A[2] and A[3], no A[4] and A[5] "played" with each other.
After that the tournament is conducted with players A[3],A[6] and A[7]. And the winner is playing with A[1] and A[0] to earn its proper spot. And so on.
At the end of this process A[0] will have the maximum element and the whole array is reorganized as a heap.
After that constructing sorted array is trivial: you swap the head of the heap with the last element of the array, shrink "unsorted" part of the array by one and reorganize heap which is now disrupted, but still partially preserves its properties, and reapply this swapping process to this unsorted part until unsorted part became just two elements.
In other words the entire HeapSort method consists of two major steps:
Wikipedia has a useful (but not perfect) animation of the process for array [ 6, 5, 3, 1, 8, 7, 2, 4 ] that I encourage to watch and try to related to the explanation above.
One practically useful application of the concept of the heap is priority queues (Heapsort):
One nice application of heaps is as a way to implement a priority queue (a data structure where the elements are maintained in order based on a priority value). Priority queues occur frequently in OS task scheduling so that more important tasks get priority for execution on the CPU. The priority queue will require operations to add new elements, remove the highest priority element, or adjust the priority of elements in the queue (updating the ordering accordingly). Thus a priority queue can be created (using BUILD-MAX-HEAP() and maintained efficiently as a max (or min depending on the application) heap. The priority queue operations are
- HEAP-MAXIMUM(A) - returns the largest (highest priority) element which for a max-heap is the root - O(1)
- HEAP-EXTRACT-MAX(A) - removes the root by swapping it with the last element in the queue (heap), decrements the size of the queue (heap), and calls MAX-HEAPIFY() on the new root (similar to a single step of heapsort) - O(lg n)
- HEAP-INCREASE-KEY(A,i,key) - modify the value of node i to key and then "bubble" it up through parent nodes (maintaining the max-heap property) - O(lg n) since at worst it will need to traverse up the entire tree lg n levels
- MAX-HEAP-INSERT(A, key) - add a new element by increasing the size of the queue (heap), setting the value of the new element to -∞, and calling HEAP-INCREASE-KEY() with the new value - O(lg n) since it takes the same time as HEAP-INCREASE-KEY()
Thus a priority queue can be created in linear time and maintained in lg time using a heap.
|
|
Switchboard | ||||
| Latest | |||||
| Past week | |||||
| Past month | |||||
MAX-HEAPIFY(A,i)
1 l = LEFT(i)
2 r = RIGHT(i)
3 if l <= A.heapsize and A[l] > A[i]
4 largest = l
5 else
6 largest = i
7 if r <= A.heapsize and A[r] > A[largest]
8 largest = r
9 if largest != i
10 exchange A[i] with A[largest]
11 MAX-HEAPIFY(A,largest)
[Aug 28, 2012] Heapsort, Quicksort, and Entropy by David MacKay
December 2005 | Cavendish Laboratory, Cambridge, Inference Group
Heapsort is inefficient in its comparison count because it pulls items from the bottom of the heap and puts them on the top, allowing them to trickle down, exchanging places with bigger items. This always struck me as odd, putting a quite-likely-to-be-small individual up above a quite-likely-to-be-large individual, and seeing what happens. Why does heapsort do this? Could no-one think of an elegant way to promote one of the two sub-heap leaders to the top of the heap?
How about this:
Modified Heapsort (surely someone already thought of this) 1 Put items into a valid max-heap 2 Remove the top of the heap, creating a vacancy 'V' 3 Compare the two sub-heap leaders directly below V, and promote the biggest one into the vacancy. Recursively repeat step 3, redefining V to be the new vacancy, until we reach the bottom of the heap. (This is just like the sift operation of heapsort, except that we've effectively promoted an element, known to be the smaller than all others, to the top of the heap; this smallest element can automatically trickle down without needing to be compared with anything.) 4 Go to step 2 Disadvantage of this approach: it doesn't have the pretty in-place property of heapsort. But we could obtain this property again by introducing an extra swap at the end, swapping the 'smallest' element with another element at the bottom of the heap, the one which would have been removed in heapsort, and running another sift recursion from that element upwards. Let's call this algorithm Fast Heapsort. It is not an in-place algorithm, but, just like Heapsort, it extracts the sorted items one at a time from the top of the heap.
Performance of Fast Heapsort
I evaluated the performance of Fast Heapsort on random permutations. Performance was measured solely on the basis of the number of binary comparisons required. [Fast Heapsort does require extra bookkeeping, so the CPU comparison will come out differently.]

Performance of Fast Heapsort.
Horizontal axis: Number of items to be sorted, N.
Vertical axis: Number of binary comparisons. The theoretical curves show the asymptotic results for Randomized Quicksort (2 N ln N) and the information-theoretic limit, log_2 N! simeq (N log N - N)/log 2.I haven't proved that Fast Heapsort comes close to maximizing the entropy at each step, but it seems reasonable to imagine that it might indeed do so asymptotically. After all, Heapsort's starting heap is rather like an organization in which the top dog has been made president, and the top dogs in divisions A and B have been made vice-president; a similar organization persists all the way down to the lowest level. The president originated in one of those divisions, and got his job by sequentially deposing his bosses.
Now if the boss leaves and needs to be replaced by the best person in the organization, we'll clearly need to compare the two vice-presidents; the question is, do we expect this to be a close contest? We have little cause to bet on either vice-president, a priori. There are just two asymmetries in the situation: first, the retiring president probably originated in one of the two divisions; and second, the total numbers in those two divisions may be unequal. VP A might be the best of slightly more people than VP B; the best of a big village is more likely to beat the best of a small village. And the standard way of making a heap can make rather lop-sided binary trees. In an organization with 23 people, for example, division A will contain (8+4+2+1)=15 people, and division B just (4+2+1)=7.
To make an even-faster Heapsort, I propose two improvements:
- Make the heap better-balanced. Destroy the elegant heap rules, that i's children are at (2i) and (2i+1), and that a heap is filled from left to right. Will this make any difference? Perhaps not; perhaps it's like a Huffman algorithm with some free choices.
- Apply information theory ideas to the initial heap-formation process. Does the opening Heapify routine make comparisons that have entropy significantly less than one bit?
The memory model assumed for this discussion is a paged memory. The N elements to be sorted are stored in a memory of M pages, with room for S elements per page. Thus N=MS.
The heapsort algorithms seen so far are not very well suited for external sorting. The expected number of page accesses for the basic heapsort in a memory constrained environment (e. g. 3 pages of memory) is
where N is the number of records and M is the number of disk blocks. We would like it to be
which typically is orders of magnitude faster. (example: 8 byte element, 4KB page, translates into 512 elements pr page).
NOTE: Be aware that the words 'page access' does not necessarily imply that disk accesses are controlled by the virtual memory subsystem. It may be completely under program control.
One may wonder if the d-heaps described in chapter 5can be used effeciently as an external sorting method. If we consider the same situation as above, it is seen that if we use the number of elements per page S as the fanout, and align the heap on external memory so that all siblings fit in one page, the depth of the tree will drop with a factor
and thus the number of page accesses will drop accordingly. As observed in the chapter on d-heaps, the cost of a page access should be weighted against the cost of S comparisons needed to find the maximal child. Anyway, because the cost of a disk access is normally much higher than the time it takes to search linearly through one page of data, this idea is definitely an improvement over the traditional heap.
The drawback of the idea is twofold. Firstly it only improves the external cost with a factor
, not the desired factor S, and secondly it increases the internal cost with a factor
. Thus it actually makes sorting much slower in the situation where all data fits in memory. Considering that gigabyte main memories are now commonplace and that terabyte memories will eventually be affordable, it is reasonable to require a good internal performance even of external methods.
Heapsort is an internal sorting method which sorts an array of n records in place in O(n log n) time. Heapsort is generally considered unsuitable for external random-access sorting. By replacing key comparisons with merge operations on pages, it is shown how to obtain an in-place external sort which requires O(m log m) page references, where m is the number of pages which the file occupies. The new sort method (called Hillsort) has several useful properties for advanced database management systems. Not only does Hillsort operate in place, i.e., no additional external storage space is required assuming that the page table can be kept in core memory, but accesses to adjacent pages in the heap require one seek only if the pages are physically contiguous. The authors define the Hillsort model of computation for external random-access sorting, develop the complete algorithm and then prove it correct. The model is next refined and a buffer management concept is introduced so as to reduce the number of merge operations and page references, and make the method competitive to a basic balanced two-way external merge. Performance characteristics are noted such as the worst-case upper bound, which can be carried over from Heapsort, and the average-case behavior, deduced from experimental findings. It is shown that the refined version of the algorithm which is on a par with the external merge sort.
www.cs.tcd.ie
[PDF]
This is what the procedure Heapify (the key procedure in Heapsort),. in effect,
does. We can describe Heapsort in template form as follows; ...
www.cs.umd.edu
There are three procedures involved in HeapSort: Heapify, Buildheap, and HeapSort
itself, ... Now at last we describe Heapsort, beginning with Heapify. ...
informatik.uni-oldenburg.de
In the figure you see the function heapsort within the functional structure of the
... The function heapsort is not called by any function of the algorithm. ...
Google matched content |
Citations Algorithm 232 Heapsort - Williams (ResearchIndex)
Princeton Computer Science Technical Reports
Analysis of Heapsort (Thesis) by Schaffer, Russel W. June 1992, 85 PagesSorting, Part 2 [PDF]
Eppstein's paper Sorting by divide-and-conquer
Priority Queues and Heapsort in Java By Robert Sedgewick Sample Chapter, Oct 25, 2002.
NIST heapsort A sort algorithm that builds a heap, then repeatedly extracts the maximum item. Run time is O(n log n). A kind of in-place sort. Specialization (... is a kind of me.)adaptive heap sort, smoothsort. See also selection sort.
Note: Heapsort can be seen as a variant of selection sort in which sorted items are arranged (in a heap) to quickly find the next item.
Author: PEB
Lang's definitions, explanations, diagrams, Java applet, and pseudo-code (C), (Java), (Java), Worst-case behavior annotated for real time (WOOP/ADA), including bibliography, (Rexx).demonstration. Comparison of quicksort, heapsort, and merge sort on modern processors.
Robert W. Floyd, Algorithm 245 Treesort 3, CACM, 7(12):701, December 1964.
J. W. J. Williams, Algorithm 232 Heapsort, CACM, 7(6):378-348, June 1964.
Although Williams clearly stated the idea of heapsort, Floyd gave a complete, efficient implementation nearly identical to what we use today.
Heapsort - Wikipedia, the free encyclopedia
Handbook of Algorithms and Data Structures
Priority Queues and Heapsort Lecture 18
Data Structures and Algorithms Heap Sort
PDF]
• Implementation
• HeapSort • Bottom-Up Heap Construction • Locators
File Format: PDF/Adobe Acrobat -
View as HTML
Java Sorting Animation Page - Heap Sort
Data Structures and Algorithms Heap Sort with nice animation
Heap sort visualization:
Java applet
Developed by Mike Copley, UH for ICS 665 (Prof. J. Stelovsky)
GNU Scientific Library -- Reference Manual - Sorting
This function sorts the count elements of the array array, each of size size, into ascending order using the comparison function compare. The type of the comparison function is defined by,
int (*gsl_comparison_fn_t) (const void * a,
const void * b)
A comparison function should return a negative integer
if the first argument is less than the second argument, 0
if the two arguments are equal and a positive integer if the first argument
is greater than the second argument.
For example, the following function can be used to sort doubles into ascending numerical order.
int
compare_doubles (const double * a,
const double * b)
{
if (*a > *b)
return 1;
else if (*a < *b)
return -1;
else
return 0;
}
The appropriate function call to perform the sort is,
gsl_heapsort (array, count, sizeof(double),
compare_doubles);
Note that unlike qsort the heapsort
algorithm cannot be made into a stable sort by pointer arithmetic. The trick
of comparing pointers for equal elements in the comparison function does not
work for the heapsort algorithm. The heapsort algorithm performs an internal
rearrangement of the data which destroys its initial ordering.
HeapSort (Docs for JDSL 2.1) Java
Less Popular Downloadable Utilities
- download Heapsort source and compiled class files to run on your own machine as a part of your own program.
Heapsort implementation unit for Turbo Pascal
Index of -ftp-benchmarks-heapsort
Heapsort in C see heapsort for the source
Heapsort.c results are included below.The program (heapsort.c) and latest results (heapsort.tbl) can be obtained via anonymous ftp from 'ftp.nosc.mil' in directory 'pub/aburto'. The ftp.nosc.mil IP address is: 128.49.192.51
Please send new results (new machines, compilers, compiler options) to: [email protected]. I will keep the results up-dated and post periodically to 'comp.benchmarks'. Any comments or advice or whatever greatly appreciated too.
Heapsort.c Test Results: MIPS is relative to unoptimized gcc 2.1 (gcc -DUNIX) instruction count using assembly output for 80486 (80386 code). The instruction count is divided by the average runtime (for 1 loop) to obtain the RELATIVE MIPS rating for memory sizes from 8000 bytes up to 2048000 bytes. These will not necessarily be like other MIPS results because the instruction mix and weightings are different! This is just a heap sort test program which I have attempted to calibrate to a relative MIPS rating. I suppose we can call this a 'HeapMIPS' rating :)
PLEASE NOTE: The Sun system results can be quite erratic unless the '-Bstatic'option is used (Sun C 2.0/3.0 comment).
HeapSort - A compact routine that sorts data in place in Basic
Manual Page For heapsort(3) BSD and Apple
Society
Groupthink : Two Party System as Polyarchy : Corruption of Regulators : Bureaucracies : Understanding Micromanagers and Control Freaks : Toxic Managers : Harvard Mafia : Diplomatic Communication : Surviving a Bad Performance Review : Insufficient Retirement Funds as Immanent Problem of Neoliberal Regime : PseudoScience : Who Rules America : Neoliberalism : The Iron Law of Oligarchy : Libertarian Philosophy
Quotes
War and Peace : Skeptical Finance : John Kenneth Galbraith :Talleyrand : Oscar Wilde : Otto Von Bismarck : Keynes : George Carlin : Skeptics : Propaganda : SE quotes : Language Design and Programming Quotes : Random IT-related quotes : Somerset Maugham : Marcus Aurelius : Kurt Vonnegut : Eric Hoffer : Winston Churchill : Napoleon Bonaparte : Ambrose Bierce : Bernard Shaw : Mark Twain Quotes
Bulletin:
Vol 25, No.12 (December, 2013) Rational Fools vs. Efficient Crooks The efficient markets hypothesis : Political Skeptic Bulletin, 2013 : Unemployment Bulletin, 2010 : Vol 23, No.10 (October, 2011) An observation about corporate security departments : Slightly Skeptical Euromaydan Chronicles, June 2014 : Greenspan legacy bulletin, 2008 : Vol 25, No.10 (October, 2013) Cryptolocker Trojan (Win32/Crilock.A) : Vol 25, No.08 (August, 2013) Cloud providers as intelligence collection hubs : Financial Humor Bulletin, 2010 : Inequality Bulletin, 2009 : Financial Humor Bulletin, 2008 : Copyleft Problems Bulletin, 2004 : Financial Humor Bulletin, 2011 : Energy Bulletin, 2010 : Malware Protection Bulletin, 2010 : Vol 26, No.1 (January, 2013) Object-Oriented Cult : Political Skeptic Bulletin, 2011 : Vol 23, No.11 (November, 2011) Softpanorama classification of sysadmin horror stories : Vol 25, No.05 (May, 2013) Corporate bullshit as a communication method : Vol 25, No.06 (June, 2013) A Note on the Relationship of Brooks Law and Conway Law
History:
Fifty glorious years (1950-2000): the triumph of the US computer engineering : Donald Knuth : TAoCP and its Influence of Computer Science : Richard Stallman : Linus Torvalds : Larry Wall : John K. Ousterhout : CTSS : Multix OS Unix History : Unix shell history : VI editor : History of pipes concept : Solaris : MS DOS : Programming Languages History : PL/1 : Simula 67 : C : History of GCC development : Scripting Languages : Perl history : OS History : Mail : DNS : SSH : CPU Instruction Sets : SPARC systems 1987-2006 : Norton Commander : Norton Utilities : Norton Ghost : Frontpage history : Malware Defense History : GNU Screen : OSS early history
Classic books:
The Peter Principle : Parkinson Law : 1984 : The Mythical Man-Month : How to Solve It by George Polya : The Art of Computer Programming : The Elements of Programming Style : The Unix Hater’s Handbook : The Jargon file : The True Believer : Programming Pearls : The Good Soldier Svejk : The Power Elite
Most popular humor pages:
Manifest of the Softpanorama IT Slacker Society : Ten Commandments of the IT Slackers Society : Computer Humor Collection : BSD Logo Story : The Cuckoo's Egg : IT Slang : C++ Humor : ARE YOU A BBS ADDICT? : The Perl Purity Test : Object oriented programmers of all nations : Financial Humor : Financial Humor Bulletin, 2008 : Financial Humor Bulletin, 2010 : The Most Comprehensive Collection of Editor-related Humor : Programming Language Humor : Goldman Sachs related humor : Greenspan humor : C Humor : Scripting Humor : Real Programmers Humor : Web Humor : GPL-related Humor : OFM Humor : Politically Incorrect Humor : IDS Humor : "Linux Sucks" Humor : Russian Musical Humor : Best Russian Programmer Humor : Microsoft plans to buy Catholic Church : Richard Stallman Related Humor : Admin Humor : Perl-related Humor : Linus Torvalds Related humor : PseudoScience Related Humor : Networking Humor : Shell Humor : Financial Humor Bulletin, 2011 : Financial Humor Bulletin, 2012 : Financial Humor Bulletin, 2013 : Java Humor : Software Engineering Humor : Sun Solaris Related Humor : Education Humor : IBM Humor : Assembler-related Humor : VIM Humor : Computer Viruses Humor : Bright tomorrow is rescheduled to a day after tomorrow : Classic Computer Humor
The Last but not Least Technology is dominated by two types of people: those who understand what they do not manage and those who manage what they do not understand ~Archibald Putt. Ph.D
Copyright © 1996-2021 by Softpanorama Society. www.softpanorama.org was initially created as a service to the (now defunct) UN Sustainable Development Networking Programme (SDNP) without any remuneration. This document is an industrial compilation designed and created exclusively for educational use and is distributed under the Softpanorama Content License. Original materials copyright belong to respective owners. Quotes are made for educational purposes only in compliance with the fair use doctrine.
FAIR USE NOTICE This site contains copyrighted material the use of which has not always been specifically authorized by the copyright owner. We are making such material available to advance understanding of computer science, IT technology, economic, scientific, and social issues. We believe this constitutes a 'fair use' of any such copyrighted material as provided by section 107 of the US Copyright Law according to which such material can be distributed without profit exclusively for research and educational purposes.
This is a Spartan WHYFF (We Help You For Free) site written by people for whom English is not a native language. Grammar and spelling errors should be expected. The site contain some broken links as it develops like a living tree...
|
|
You can use PayPal to to buy a cup of coffee for authors of this site |
Disclaimer:
The statements, views and opinions presented on this web page are those of the author (or referenced source) and are not endorsed by, nor do they necessarily reflect, the opinions of the Softpanorama society. We do not warrant the correctness of the information provided or its fitness for any purpose. The site uses AdSense so you need to be aware of Google privacy policy. You you do not want to be tracked by Google please disable Javascript for this site. This site is perfectly usable without Javascript.
Last modified: March 12, 2019