Midnight Commander tutorial

For sysadmins who want to pass RHCSA exam

by Dr. Nikolai Bezroukov

• Abstract
• Introduction
• Invocation
• Directory Navigation
• File Selection
• Basic File Operations
• Built-in file viewer
• Built-in editor
• User menu
• Changing listing mode on panels
• Searching for files
• Comparing the content of two directories
• Directories Hotlist: Ctrl-\
• Using  external editor as background process in full console mode
• Transferring macrovariables defined on panels to subshell
• Learning more

Abstract

This tutorial is oriented mainly on qualified Linux sysadmin who reaching of striving to reach the level which allow them to be certified as Rhcsa

As Linux grow in complexity working with command line became more and more difficult.  Because command line environment provides limited visual feedback and does not display the content of the current directory or set of files you are manipulating you need to resort to frequent use of ls command.  Typos in file names can be devastating, if you are working as root.

There is no perfect cure for this problem, but using Midnight Commander does help to avoid some types of blunders. It also increases your productivity which is important in stressful situations such as exam or emergency. This program is not installed by default, but can be installed in 10 seconds from Red Hat ISO. Learning how to use it involved steep learning curve, but you efforts are paid quickly by the increase of speed and correctness of your operation on files and better understanding of the systems you maintain.

Midnight Commander belongs to the type of file managers which are called Orthodox file manager and originated from MS DOS in 1984 with Norton Commander.  the interface used in it allow generating commands dynamically from elements of GUI and as such represents more flexible and powerful environment that typical file managers. In a way, it can be viewed as a visual shell for Linux/Unix.

Introduction

1. All basic file operations including move, copy, rename, delete, chown, link, view, and edit
2. Working with normal interactive shell window (Ctrl-O). Visually it looks like you hide two panels and expose the third windows hidden underneath.

   NOTE:  If you are using the bash shell, keep in mind that non-login interactive shells only source your ~/.bashrc file (and not the ~/.bash_profile file) which means that if you have aliases or other customizations that you want to use then you should put these in ~/.bashrc.
    

3. A built in Virtual File System that allows browsing of archives such as tar, compressed tar, rpm, deb, zip, cpio, etc files as well as remote files via FTP and SFTP
    
4. Mouse support both at the Linux console (via the gpm mouse service), terminal emulators and GUI.
    
5. A good, perfectly usable Windows-style text editor (superior to pico and more "Windows-friendly" then vim). 
    
6. File viewer capable to viewing very large files and provide "intelligent" rendering of manpages, html files and more. Provided functionality is approximately the same as a typical subset used by most people with  less (which is more powerful but at the same time more obscure viewer).
    
7. Support for external viewers and editors, which can be individualized based on extension. 
    
8. Built in Find File capacity and ability to create a virtual panel out of found files. Each file on the panel can be processed like on regular panel (F3-F6,F8 work on those file like on normal files)
    
9. Directories bookmarks (called directories hotlist in mc)
    
10. The ability to compare and sync directories.
     
11. Online help system
     
12. User menu which can serve as collection of script implementing frequently used custom operations, programmed using bash with parameters supplied by Midnight commander (see below).

As with any powerful programs, you need to start with the basic subset and gradually increase the set of operations you are using. I hope that you will find mc  for Rhcsa exam, where is can save at least a dozen of minutes and thus increase your chances of passing the exam.  But I hope you can use it in your daily work too.

Invocation

If Midnight Commander started as mc it presents to the user idiosyncratic two panel screen, which is the hallmark of this type of file managers. Tqo directories displayed can be changed and them remembered for the next invocation.  For example (here mc is running in one of screen sessions) :

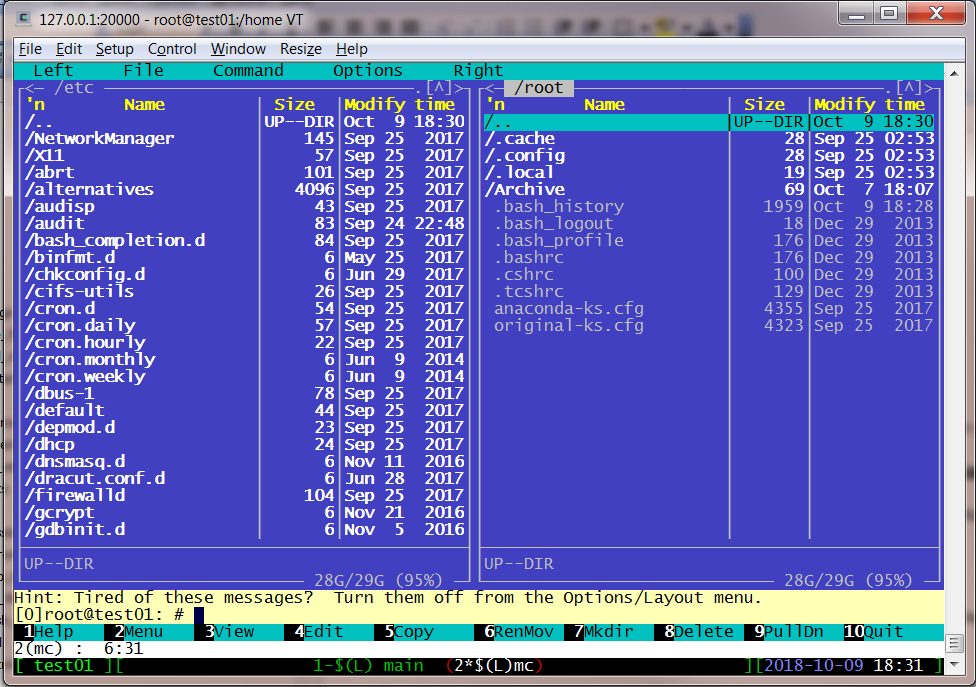
If pseudo graphic characters are mangled and you use terminal emulator the first thing is to change font.   You can also use mc without psedoggraphic by using option -a on invocatin:

mc -a

If you move the mouse around you should also see a pointer moving on the screen. If you don't see a cursor when using mc at the console then make sure that the gpm  service is running. 

This main screen  consists of five  components:

1. The menubar at the top which contains drop-down menus. If  is activated by pressing F9 or clicking with the mouse it, or on the label F9 at the bottom of the screen. Pressing F10 bring the menu allow to exist the commander.  F2 provides user menu which consists of small useful scripts and can be customized to your needs.  Each script is assigned a hotkey using which it is invoked. For example in default configuration F2-3 invoke tar which creates gzipped archive of the current directory in the parent directory. Default name of the archive is the name of the directory but you can change that as it presents a dialog box.
2. Two directory panels each of which displays file listings of the a directory. One with cursor in it is called current or active. It is are scrollable with Up/Down keypair, or PgUp/PgDown. The another -- passive or inactive.  mc is normally run in this two-panel mode although single panel mode is also supported (modes can be switched using Alt-T in circular fashion).  The directory panels display the content of two directories and are called left and right panel. With one of them being the "current directory." File operation are performed on files in this current directory. Copy, rename, and move operations by default are the non-current directory ("passive") directory the "target" for the operation. To select one directory panel simply click the mouse anywhere in the panel. You can also use the TAB key to switch the current directory from one panel to the other.
3. A "hint line"  Below panel separator (made of pseudographic characters) is the hint line which displays a series of hints and also some error messages.  You can suppress it in settings via F9-O-L (which actives Layout menu in Options and disabling hint bar)
4. The command line. This is the line below the hint line is so called on which you can type shell commands using macrovariables defined by Midnight Commander for the current configuration of the panels. Most important are as %f (current file). %F (same in the passive panel), %d (the current directory), %D (the same on passive panel), %t (list of selected files).  Command runs as if you if you'd entered it at the shell prompt but unless you put pause at the end you will not see error messages
5. Function key labels. They at the bottom of the screen and are clickable by mouse. They are useful not only for  a newbie, but also when F keys are not working in your particular setup (Esc-1, Esc2... is another alternative in this case). F1 -- Help menu, F2 --  User Menu, F3 -- view a file, and so on.  If F keys do not  work this is an alternative that can be used.  Again, another option is to use Esc-1... Esc-10 sequences instead. Also if some key is not working might try to ask Midnight commander to "learn" this key via F9-O-K (Lean key item in options menu) but in my practice that rarely helps.

Directory Navigation

• Select a directory on the current panel and hit Enter key. You also can click on it with the mouse
  • Note: mouse wheel typically works and allows quick navigation to desired file or directory within the panel
  •  Quick search is activated with Ctrl-S and allow selection using the minimal prefix.
• Use the cd command in the command line
  • Note:  The command line provides expansion of tile character i.e., entering cd ~/bin would change to the bin directory in your home directory. Also, clicking on the ".." entry will move to the current directory's parent as will entering cd .. on the command line. There is also a Directory History (alt-H) and Directories hotlist (Ctrl-\) that speed directory navigation. Directories hotlist allow creation of any number of favorites

Tab changes the current panel. The old other panel becomes the new current panel and the old current panel becomes the new other panel. The selection bar moves from the old current panel to the new current panel.

Ins key allow to tag files under cursor (after that you can copy a group with F5 or move with f6 command) you may use the Insert key (the kich1 terminfo sequence).

TIPS:

• You can quickly switch passive pane into active by using the TAB key (or Ctrl-I).
• You can also swap panels using Ctrl-U; note that the currently active directory does not change.
• To refresh the directory display use Ctrl-R

To change the sort order of the files being displayed, use the Sort Order  menu item (F9-L-S, F9-R-S). This allows you to sort files by name, size, various time stamps, inode number, and so forth. You can also specify whether sorting should be case (in)sensitive or reversed.

Sorting by size is very useful when trying to cull out files to recover disk space; sorting by date is useful when you are searching for a recently installed, created, or modified file in a directory with many files or are looking for ancient files that can safely be warehoused.

As with sorting, use the F9-L-F  menu item to filter non relevant files from the view of the directory listing using shell patterns. For instance, suppose that you wanted a listing containing only files with a .conf extension in /etc directory. In the Filter dialog simply enter "*.conf" and all other files are removed from the listing. This is very useful when you wish to work with only a subset of files in a directory in an uncluttered setting.

You can also cycle from two-panel to single-panel modes using Alt-T. This is particularly useful when you have files with very long file names and need to see them.

NOTES:

• You can use the F9-L-L (F9-R-L)  menu item (Listing Mode) to customize what which file attributes the panel lists.  The proper names for "typical" attributes in mc are name, size, perm, owner, group, mtime. Do not touch the first two system names (half and type) while editing this line. 
• You can resize the panels using the F9-O-L  menu item ("Layout"). This allows you to split the panels either vertically or horizontally as well as set the unequal number of columns for each panel using the ">" and "<" keys.  That later is useful if you are working on small screen such on 12" laptop. In this case one panel can have all attributes and the other just name, size and date.

File Selection

First, we need to make a distinction between the currently selected file or directory and marked or tagged files. The currently selected file is simply the one that is highlighted in the current directory panel. If you want to delete one file simply move the highlight bar to that file and hit F8 to delete it. However, if you want to delete a group of files then you'll need to tag them first.

NOTE: you can specify "save deletion" in MC. In this case it will organize Windows style Trash can. to enable this mode use F9-O-C and click of "safe delete option in the menu.

Tagging can be done in a couple ways. The simplest is to click Ins key on the file or directory

If the files you want can be specified by a shell pattern :

1. To select a group of files by pattern hit the "+" key. This will cause a dialog box to appear in which you can enter the search pattern. Note that entering the "*" wildcard will select all the files in the directory.
2. To select all the files in the directory hit the "*" key. This has the same effect as using the + key and then entering "*"
3. To unselect a group of files hit the "\" key or the "-" key. A dialog box similar to that with the + key will appear; if you want to unselect all files then enter "*"

Using pathname expansion (also known as filename globbing) you can form a group of  similar files for subsequent  operations on them (if there is group of file selected F5, F6 and F8 work with this group not with the current file). mc allows you to specify several globbing patterns separated with ';'

You selections and position of your cursor on the panel (the current file or directory), and directories displayed by active and passive panel automatically are reflected in built-in macrovariables, which can be used on command line and in user menu. The most important macrovariables are %f, %d and %t (for the active panel) and their counterparts for the passive panel

1. %p -- name of the current file. (without path, but remember that $PWD is the path to the current  directory, so the value of %d is available instantly after you entered shell screen)
2. %f -- name of the current file for non-local VFS. %F the same on the passive panel. Unlike %p, if file is located on a non-local virtual filesystem, i.e. either tarfs, mcfs or ftpfs, then the file will be temporarily copied into a local directory and %f will be the full path to this local temporal file. If you don't want to get a local copy and want to get the full path to the file located at the virtual FS then use %d/%p instead
3. %s and %S -- The tagged files if there are any. Otherwise the current file.
4. %x -- The extension of current file name.
5. %b -- The current file name without extension.
6. %d -- The current directory name. %D -- same on passive panel
7. %t -- The currently selected files. %T --The selected files in the passive panel.
8. %u and %U  Similar to the %t and %T macros, but after execution of this macros the selection is removed. That means you can use this macros only once in a menu item as the next time there is no any selected files in the panel.
9. %s and %S If selected files exist them the list of selected files, otherwise the current file. 

Here is an example of usage of %D macro variable in user menu:

T     Copy current directory to other panel recursively
      tar cf - . | (cd %D && tar xvpf -)

Basic File Operations

mc allow transparently go into gzipped tarballs and regular tarballs by just clicking enter, as if it is a regular directory.

Below is a short summary of the file operations. In the next section we'll look specifically at file viewing and editing. Keep in mind that while the summary below indicates the keystrokes for the various operations, all of these can be accessed using the "File" menu (those opration also are displaed as labels at the bootm, so you ca use is as instant help):

 F5: copy

Normally, to copy a file from one directory to another select or tag the file (s) to copy in the current directory panel and change to the target directory in the other directory panel. Hit F5 or click on the Copy function at the bottom. Doing so brings up a dialog box:

If you want to use a different directory than the one in the other panel or if you want to change the file name then you can use the to: entry box to do so.

Also, when you perform a copy (and move or delete) operation mc displays a dialog box with a progress meter indicating the progress on the current file as well as the overall progress if a set of files has been selected.

 

F6: move/rename

These are very similar to the copy operation described above in that the destination directory defaults to the non-current directory in the case of the move operation. Note that renaming a file entails "moving" it to another filename. In this case, use the to: entry field in the dialog box to enter the new filename.

F7: mkdir:

While not a file operation per se, the mkdir command allows you to create a new directory in the currently active directory. A dialog box is presented that will prompt you for the new directory name.

F8: delete

After selecting or tagging a file or set of files hit F8 to delete them. Note that you'll be asked for confirmation. Also, mc is able to recursively delete a directory, but this, too, requires confirmation. If you're having to clean out a directory then I'd strongly suggest your using mc. It makes selecting files very easy and helps prevent costly accidental deletions.

Note: that at any time you can cancel an operation by hitting the Escape key twice.

You can also work with links:

• F9-F-L (hard) link   A dialog box will prompt you for the filename for the newly created link.
• F9-F-S  (symbolic link)    A dialog box will prompt you for the filename for the newly created link.

Chown and chmod operation is also available via F9-F-C and  F9-F-O  key combinations. A dialog box is presented that will allow you to select owner and group from a list of valid values. Note that an "Advanced Chown" facility is available under the "File" menu. Until you're rather sure of what you're doing, this is probably best left alone.

With these functionality you'll be able to do a good deal of day to day file system maintenance and sysadmin tasks.

Built-in file viewer

• F2  toggles line wrapping
• F3  exit the viewer
• F4  toggle hex view mode
• F5  goto line; a dialog box appears which will prompt you for a line number
• F6  regular expression search
• F7  normal search
• F8  toggle raw or parsed mode
• F9  toggle formatted or unformatted mode: this affects attributes such as bold or underline which are displayed using various colors
• F10  exit the viewer

Viewer provides "intelligent" formatting support for several common file formats including manual pages, HTML, and mail file. That is better than viewing the raw file. 

Viewer also can search for regular expression  on the file (F6). In addition Ctrl-s  and Ctrl-r  can be used for normal or reverse searches. Once you've started a search, hit the letter n  to find the next match. Ctrl-l  will repaint the screen; Alt-r  will toggle the display of a ruler.

For example, to view a manual page (which are normally gzipped ) simply select the file and hit F3. You can do similar things with HTML files and several other formats. In the case of HTML files it is worth noting that "viewing" file of console in text mode is by definition inferior to viewing HTML files in a regular web browser  in the GUI environment; mcviewer just strip out the hypertext tags and use colors to denote links and such.

The internal file viewer also give you an ability to view files in hex mode. 

In terms of moving around the file you can use mouse wheel and/or there are multiple shortcuts:

• Space, Page Down  - move forward one page
• Page Up, or b  - move back one page
• Home, Alt-<  - move to head of file
• End, G, Alt->  - move to end of file
• up/down arrows  - move forward or backward a single line
• Ctrl-n, Ctrl-p  - move forward or backward a single line
• left/right arrows  - scroll horizontally

NOTE: If you are in View mode and hit Ctrl-F  then the viewer will move to the next file in the directory and display it. In this way you can easily move through a set of files, viewing one right after the other.

Built-in editor

The internal file editor provides a full set of editing features and can be used to edit both text and binary files up to a size of 16 megabytes.  See mcedit for more details.

like mc it has top menu, but by default it is hidden and became visible only if you press F9 key.  Due to its DOS-style behavior the editor can be used by most PC users with almost zero learning curve. Some highlights:

1. F3 starts selection of line block. After that you can expand the block iether up or down. The second  F3 freeze the block and copy is into internal buffer. After that you can iether copy or move it with  F5 and F6 correspondingly.
2. Undo. The editor provides multilevel undo capability (Ctrl-U)
3. Top menu. Like all Dos/Windows-style editors, mcedit has the top menu. Like the top menu in OFM managers it is normally hidden, but can be made visible by pressing F9 key.
4.  The editor some unique capabilities due to existence of editor user menu (cedit.menu in mc version 4.8 renamed to mcedit.menu), including the ability to insert the content of the file instead of the current selected block or position of the cursor, if no block is selected (%b macro, see below).
5. The editor supports macros (see below). To define a macro,
   • Press Ctrl-R  and
   • Then type out the keys you want to be executed.
   •  Press Ctrl-R  again when finished.
   • You can then assign the macro to any key you like by pressing that key.
   The macro is executed when you press Ctrl-A  and then the assigned key. The macro is also executed if you press Meta, Ctrl, or Esc and the assigned key, provided that the key is not used for any other function. The macro commands are stored in the special file ~/.mc/cedit/cooledit.macros. Do NOT edit this file if you are going to use macros again in the same editing session, because mcedit  caches macro in memory. mcedit  now overwrites a macro if a macro with the same key already exists, so you won't have to edit this file. You will also have to restart other running editors for macros to take effect.
6. Built-in code formatting and spellchecking.
7. There is a bottom menu that shows F-keys assignments. All items in this menu are clickable by mouse. No ability of "rolodex" -- to change the menu when you press  Ctrl-, Alt- and Shift- keys.
8. Syntax highlighting. The editor provided user customizable syntax highlighting for all major scripting and programming languages (you can create your own highlighting scheme).
9. Two types of search and replace
   • Regular expression search and replace
   • MC-specific scanf-printf search and replace. You can use scanf search and replace to search and replace a C format string. First take a look at the sscanf  and sprintf  man pages to see what a format string is and how it works. Here's an example: suppose that you want to replace all occurrences of an open bracket, three comma separated numbers, and a close bracket, with the word apples, the third number, the word oranges and then the second number. You would fill in the Replace dialog box as follows:

     Enter search string
     (%d,%d,%d)
     Enter replace string
     apples %d oranges %d
     Enter replacement argument order
     3,2

     The last line specifies that the third and then the second number are to be used in place of the first and second.

     It is advisable to use this feature with Prompt On Replace on, because a match is thought to be found whenever the number of arguments found matches the number given, which is not always a real match. Scanf also treats whitespace as being elastic. Note that the scanf format %[ is very useful for scanning strings, and whitespace.

User menu

The format of the menu file is very simple: items are separated with the blank line(s) and consist of blocks of indented line with a header:

• Header. The header is one or more lines that starts with at position 1 of the line with no leading spaces. Header consists of two parts:
  • Visibility conditions: predicates which are evaluated. If they are true the menu item will be displayed, otherwise it will be skipped.
  • Shortcut: this is the last line of the header (and can be the only line as conditions are optional). The first word in this line is hotkey. This hotkey can be any symbol on the keyboard (not only letter). For example . (dot) or ~ (tilde) are legitimate hotkeys.
     
• Body. The body consists of one or more shell statements and starts with one or more spaces or tab.  If user selects the particular menu item with the hotkey all the lines that start with a space or a tab will be copied to a temporary file. All macro symbols will be expanded and then the file with be executed as if it is a regular bash script.  This allows the user to put arbitrary shell constructs in the menus and also call or source other shell scripts. Macro substitution takes place before executing the menu code. 

Let's look into a simple example:

i   Display ipconfig information
    ifconfig -a

I   Display ipconfig man page
    man ifconfig 

In this case we see two menu items with headers consisting of a single like and containing no visibility predicates. That means that those items will always be displayed in the menu.  You can use macrovariables as ordinary shell variables

X Extract the contents of a compressed tar file

    tar xzvf %f

Here is a more interesting example that uses %D macrosymbol: 

J Copy current directory to other panel recursively

    tar cf - . | (cd %D && tar xvpf -)

The menu can also contains comment blocks that are started with '#'. The additional comment lines must start  space or tab.  That permit temporary deletion of the items from the menu

This is essentially the functionality similar to Windows Start menu. Although it was invented before Windows (in 1986 with version 1.p0 of Norton Commander it is more flexible as entries are arbitrary scripts..  But what makes is far superior is visibility predicated and ability to use macrovariables. With visibility predicates instead of one static menu MC users set a set of different menues depending of context existing in the panel. For example if the panel does not contain selected files all entries related to this context will be excluded.

There is also ability to overwrite more global entries with more local, specialized entries.  When the user presses F2, mc checks in three places to find a menu,. The first found menu is used:

• first mc checks for the existence of the file .mc.menu in the current directory. It is used if and only if it is owned by the current user or root and is not world-writable.
• second the existence of the file ~/.mc.menu is checked. the same ownership and permission check as in previous case is performed. used.
• system wide menu (the default menu) at  /usr/share/mc/mc.menu is used. This menu is created during the mc installation and can be modified by the user to suit his/her needs.

The fact that mc checks for ownership and rights provide the possibility dynamically switch from the user menu to system wide menu and back: to hide user menu from the path all you need is just to change permission to 000. 

Let's look into slightly more complicated example:

v     Edit the current file using vim 
       vim %f

V     Edit all selected
       vim %t

It is clear that if there are selected files we probably do not need the item that edits a single file and we can both mark with the same hotkey "v". 

For more information see MC Context Sensitive User Menu

Changing listing mode on panels

To save you new setup you need to use F9-O-S ("Save setup" item in Options menu).

Searching for files

Searching for files is common task  for any Linux sysadmin and mc implements several types of such search which in many cases are more convenient that using  find and grep.

Unique type of search implemented by mc is a local search of file in the current directory using prefix that you type one letter at a time with visual feedback of the result of search of this prefix after each typed letter on the panel (in the manner invented by Norton Change Directory(NCD) from Norton Utilities for DOS) and two types of global search. This is very handy when searching for a particular file in a large directory like /etc

1. Filename search with visual feedback after each typed letter using prefix can be invoked using shortcuts Ctrl-S, or Alt-S. It uses mini-status box at the bottom of each directory panel to display typed prefix.  By hitting Ctrl-S or Alt-S the status box becomes an entry box in which you type in a file or directory name to search for. As you type, mc does an incremental search and automatically selects the file which matches the search.
2. Global file search. There are two way for searching for file "globally" (using as root for search any directory you like) in mc:
   • Simple search (F9-Alt-? or Alt-Shift-?)  which allow to use regular expressions and produced the list on the screen. After list is displayed
   •  you have an option to view it in the built-in viewer, to edit it in the built-in editor or panelize it.
   • External panelize when you can provide arbitrary command or script which should provide the list of file with full path names and they will be displayed in virtual panel as if they belong to a single directory. You can move those files, delete them, change attributes, rename them, edit as if this is a normal panel displaying a directory.   In other words mc create a virtual filesystem out of files that are output of the particular command.

Mc also can search for a string or a regular expression inside files combining find and grep functionality.

Comparing the content of two directories

The key combination F9-C-C compare "active" directory in one panel with the "passive" on another. It is so useful that actually etched in the brain of advanced mc users. This will pop up a dialog box that allows you to select the type of directory comparison: Size simply compares files by size; Quick compares files by size and date; and byte-by-byte comparison. After the comparison operation is complete  different file with be highlighted and (if you are sure that current directory is the one with newer files) you can copy files that are different to passive directory using single press of F5 key.

Directories Hotlist: Ctrl-\

Use this to create a popup hotlist of frequently accessed directories. The hotlist keeps a list of "alias-directory path" pairs. For example, if you use ~joeuser/personal/ to store your personal programming projects then you could create an entry using the "New Entry" option and alias it to something like "Personal Projects".

If you use mc as an ftp client then you can use the directory hotlist to keep the URL's for your frequented sites! To edit (add, modify, or delete entries) the list type in Ctrl-\ and then use "New Entry" to create a new entry: enter the URL for the site, including the path to the directory that you're interested in and then fill in the alias. Now, anytime that you need to ftp just popup the hotlist and select the site!

Using external editor as background process  in full console mode

One way to quickly create the "all-in-one-command-center" is execute mc and then start a subshell. From it you can invoke vim  with the file on which you are working and hit Ctrl-Z to stop its execution and put it in the background. This returns you to the shell. Now, if you need to run mc then hit Ctrl-O; if you need to use your editor to make chances in config file or script, type in fg which will resume the stopped program; and if you need to run any other program then use the shell as normal. This is a powerful means of increasing your productivity during crammed environment if you and can't open multiple terminal on your display. 

NOTE: This tip was first described by John M. Fisk in his An Introduction to the Midnight Commander (Vanderbilt University, October, 1997.)

Transferring macrovariables defined on panels to subshell

You can transfer macrovariables available on panels to subshell via wring them to file as variables (using a small script  put as a item in the user menu; the script should write the values of those variables in the form of export statements into your home directory), and then sourcing this file in subshell, but  that requires some work and, preferably, programmable keyboard (if you access console from Terminal emulator such  as Putty any Microsoft keyboard will suit, as Intellitype can be installed to provide several macros on them; if you use Teraterm as terminal emulator, Teraterm macros can also be used without programmable keyboard)

Learning more

There are also several good tutorials on the web which described the program from slightly different angles (not necessary oriented on qualified Linux sysadmin who wants to be certified as Rhcsa and might wish to use it during exam, like this tutorial):

• Midnight Commander Guide by  Mueen Nawaz, Sep 23, 2012. This is so far the best tutorial I have found on the WEB. It even contains some troubleshooting tips
  •  Local copy (I am just afraid that it will disappear):  Midnight Commander Guide by  Mueen Nawaz, Sep 23, 2012
• MC Tutorial by Jane Trembath (last modified in 2018, so it is current). This tutorial is oriented on complete novices.
• An Introduction to the Midnight Commander  by John M. Fisk <[email protected]> October, 1997 Nashville, TN  An old, but still good academic-style overview.

Recommended Links

Softpanorama Recommended

Top articles

Sites

• Cheetsheet for Midnight Commander
• Midnight Commander version 4.8
• MC Extension menu
• External panelize
• MC Macro Variables
• MC Context Sensitive User Menu
• Midnight Commander Tips and Tricks
• mcdiff -- Midnight Commander diff viewer
• mcedit
  • MC editor macros and user menu
  • mcedit keymap
• mcview
• Midnight Commander's color scheme
• MC does not display pseudo-graphic characters properly
• Changing the Listing Format in MC

Etc

Society

Groupthink : Two Party System as Polyarchy : Corruption of Regulators : Bureaucracies : Understanding Micromanagers and Control Freaks : Toxic Managers :   Harvard Mafia : Diplomatic Communication : Surviving a Bad Performance Review : Insufficient Retirement Funds as Immanent Problem of Neoliberal Regime : PseudoScience : Who Rules America : Neoliberalism  : The Iron Law of Oligarchy : Libertarian Philosophy

Quotes

War and Peace : Skeptical Finance : John Kenneth Galbraith :Talleyrand : Oscar Wilde : Otto Von Bismarck : Keynes : George Carlin : Skeptics : Propaganda  : SE quotes : Language Design and Programming Quotes : Random IT-related quotes :  Somerset Maugham : Marcus Aurelius : Kurt Vonnegut : Eric Hoffer : Winston Churchill : Napoleon Bonaparte : Ambrose Bierce :  Bernard Shaw : Mark Twain Quotes

Bulletin:

Vol 25, No.12 (December, 2013) Rational Fools vs. Efficient Crooks The efficient markets hypothesis : Political Skeptic Bulletin, 2013 : Unemployment Bulletin, 2010 :  Vol 23, No.10 (October, 2011) An observation about corporate security departments : Slightly Skeptical Euromaydan Chronicles, June 2014 : Greenspan legacy bulletin, 2008 : Vol 25, No.10 (October, 2013) Cryptolocker Trojan (Win32/Crilock.A) : Vol 25, No.08 (August, 2013) Cloud providers as intelligence collection hubs : Financial Humor Bulletin, 2010 : Inequality Bulletin, 2009 : Financial Humor Bulletin, 2008 : Copyleft Problems Bulletin, 2004 : Financial Humor Bulletin, 2011 : Energy Bulletin, 2010 : Malware Protection Bulletin, 2010 : Vol 26, No.1 (January, 2013) Object-Oriented Cult : Political Skeptic Bulletin, 2011 : Vol 23, No.11 (November, 2011) Softpanorama classification of sysadmin horror stories : Vol 25, No.05 (May, 2013) Corporate bullshit as a communication method  : Vol 25, No.06 (June, 2013) A Note on the Relationship of Brooks Law and Conway Law

History:

Fifty glorious years (1950-2000): the triumph of the US computer engineering : Donald Knuth : TAoCP and its Influence of Computer Science : Richard Stallman : Linus Torvalds  : Larry Wall  : John K. Ousterhout : CTSS : Multix OS Unix History : Unix shell history : VI editor : History of pipes concept : Solaris : MS DOS :  Programming Languages History : PL/1 : Simula 67 : C : History of GCC development :  Scripting Languages : Perl history   : OS History : Mail : DNS : SSH : CPU Instruction Sets : SPARC systems 1987-2006 : Norton Commander : Norton Utilities : Norton Ghost : Frontpage history : Malware Defense History : GNU Screen : OSS early history

Classic books:

The Peter Principle : Parkinson Law : 1984 : The Mythical Man-Month :  How to Solve It by George Polya : The Art of Computer Programming : The Elements of Programming Style : The Unix Hater’s Handbook : The Jargon file : The True Believer : Programming Pearls : The Good Soldier Svejk : The Power Elite

Most popular humor pages:

Manifest of the Softpanorama IT Slacker Society : Ten Commandments of the IT Slackers Society : Computer Humor Collection : BSD Logo Story : The Cuckoo's Egg : IT Slang : C++ Humor : ARE YOU A BBS ADDICT? : The Perl Purity Test : Object oriented programmers of all nations : Financial Humor : Financial Humor Bulletin, 2008 : Financial Humor Bulletin, 2010 : The Most Comprehensive Collection of Editor-related Humor : Programming Language Humor : Goldman Sachs related humor : Greenspan humor : C Humor : Scripting Humor : Real Programmers Humor : Web Humor : GPL-related Humor : OFM Humor : Politically Incorrect Humor : IDS Humor : "Linux Sucks" Humor : Russian Musical Humor : Best Russian Programmer Humor : Microsoft plans to buy Catholic Church : Richard Stallman Related Humor : Admin Humor : Perl-related Humor : Linus Torvalds Related humor : PseudoScience Related Humor : Networking Humor : Shell Humor : Financial Humor Bulletin, 2011 : Financial Humor Bulletin, 2012 : Financial Humor Bulletin, 2013 : Java Humor : Software Engineering Humor : Sun Solaris Related Humor : Education Humor : IBM Humor : Assembler-related Humor : VIM Humor : Computer Viruses Humor : Bright tomorrow is rescheduled to a day after tomorrow : Classic Computer Humor

The Last but not Least Technology is dominated by two types of people: those who understand what they do not manage and those who manage what they do not understand ~Archibald Putt. Ph.D

The statements, views and opinions presented on this web page are those of the author (or referenced source) and are not endorsed by, nor do they necessarily reflect, the opinions of the Softpanorama society. We do not warrant the correctness of the information provided or its fitness for any purpose. The site uses AdSense so you need to be aware of Google privacy policy. You you do not want to be tracked by Google please disable Javascript for this site. This site is perfectly usable without Javascript.

Last modified: December 13, 2020